Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






V. Вычисление доверительных интервалов для математического ожидания и дисперсии

⇐ ПредыдущаяСтр 43 из 89Следующая ⇒

 

1. Так как гипотеза о нормальном распределении случайной величины 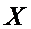не противоречит опытным данным, то будем считать (с некоторым риском), что случайная величина 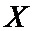распределена нормально, причем математическое ожидание 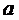и среднее квадратическое отклонение 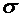этого распределения неизвестны.

Доверительный интервал для оценки математического ожидания имеет вид:

 

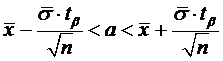
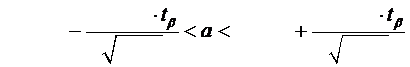
По доверительной вероятности 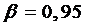и числу степенной свободы

 

69

 

находим (например, В.Е.Гмурман “Руководство к решению задач по теории вероятностей и математической статистике” приложение3) величину

 

1,99,

а затем точность оценки

 

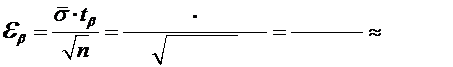0,02.

 

Итак, получим искомый доверительный интервал, покрывающий неизвестное математическое ожидание с заданной надежностью 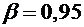, т.е. интервал

 

 

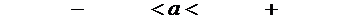
4,50 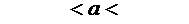4,55

 

2. Доверительный интервал для 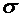имеет вид:

 

,

 

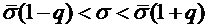0,0871 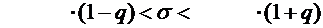*0,0871

 

Для 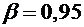и 70 по таблице (см. в учебниках В.И. Ермаков “Сборник задач по высшей математике для экономистов” приложение 3 стр. 520 или приложение 4 В.Е. Гмурман “Руководство к решению задач по теории вероятностей и математической статистике”) находим

 

0,172

 

Отсюда

 

 

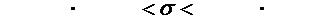
0,0721 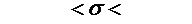0,1021

 

Поясним смысл, который имеет заданная надежность 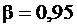. Из 100 выборок 95 определяют такие доверительные интервалы, в которых параметр ( 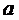и 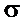) действительно заключен, и только в пяти выборках он может выйти за границы доверительного интервала.

 

 


⇐ Предыдущая38394041424344454647Следующая ⇒





Date: 2015-07-27; view: 687; Нарушение авторских прав


mydocx.ru - 2015-2025 year. (0.01 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию