Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
ЗАДАЧА №3
|
|
Определить величину эмпирического корреляционного отношения, если общая дисперсия: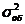 
=15,2, групповые средние 
; 
; 
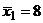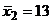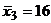, а численности групп соответственно равны 75; 60 и 65.
Тема 3. Моделирование вариационных рядов.
Вычисление теоретических частот кривой
нормального распределения
Распределение непрерывной случайной величины х называют нормальным (N (
,s)), если соответствующая ей плотность распределения выражается формулой:
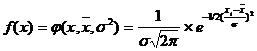
Этап 1. Расчет по эмпирическим данным параметров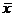 
, 
.
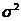Этап 2. Расчет нормированных отклонений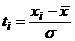 
.
Этап 3. По таблице распределения функции f(t) найти значения функции.
Этап 4. Вычисление теоретических частот 
по формуле:
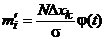
Этап 5. Оценка расхождений частот эмпирических и теоретических на основе критериев согласия. Критерий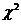 
(хи-квадрат) Пирсона.
Размер жилой площади на члена семьи,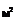 
| Число семей
| Середина интервала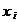 
|
|
| 
|
|
| 
|
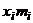
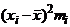
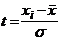
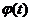
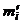
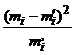
| А | ||||||||
| До 5 | 494,52 | -2,37 | 0,0241 | 0,33 | ||||
| 5 – 7 | 378,74 | -1,89 | 0,0669 | 1,0 | ||||
| 7 – 9 | 600,83 | -1,31 | 0,1456 | 2,04 | ||||
| 9 – 11 | 622,52 | -0,83 | 0,2565 | |||||
| 11 – 13 | 204,28 | -0,46 | 0,3589 | 0,18 | ||||
| 13 – 15 | 0,21 | 0,01 | 0,3989 | 2,96 | ||||
| 15 – 17 | 232,27 | 0,49 | 0,3538 | 0,31 | ||||
| 17 – 20 | 18,5 | 746,93 | 1,08 | 0,2203 | ||||
| 20 – 25 |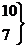 
| 22,5 | 731,88 | 2,04 | 0,0498 |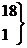 
| 0,21 | |
| Свыше 25 | 27,5 | 192,5 | 1286,17 | 3,23 | 0,0021 | |||
| Итого | 4183,5 | 5298,35 | 10,03 |
Рассчитать теоретические частоты кривой нормального распределения на основе распределения семей по размеру жилой площади на члена семьи.
| Решение |
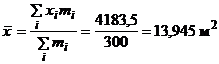
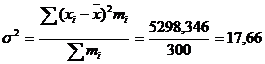
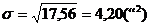
k = 1,2... 7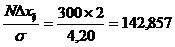 
при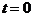 
(
) 
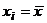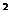стандартизованная функция
k = 8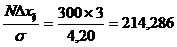 
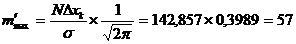
k = 9,10 
При распределении частот по серединам интервалов может быть нарушено условие равенства сумм эмпирических и теоретических частот.
После вычисления теоретических частот необходимо оценить степень близости теоретических и эмпирических частот. Выдвигается гипотеза о том, что расхождение между теоретическими и эмпирическими частотами носят случайный характер. Эту гипотезу можно проверить с помощью критерия согласия Пирсона .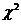
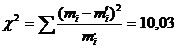или 
,
где 
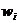и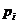 
– соответственно частости эмпирического и теоретического распределения.
Рассчитанное значение 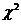сравнивается с 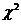табличным. Для выбранного уровня значимости (как правило, a = 0,05) и при данном числе степеней свободы (u) определяется критическое значение критерия согласия 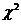критическое.
u = К(число групп) – число связей (з) = 9 – 3 = 6
Теоретические частоты должны удовлетворять трем условиям:
; 
; 
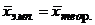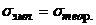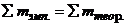
a – уровень значимости, выражает вероятность того, что будет отвергнута правильная гипотеза.
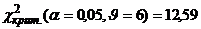
Так как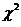 
расч. < 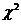крит., то заключаем, что опытный ряд хорошо согласуется с гипотезой о нормальном распределении, нулевая гипотеза о случайном характере расхождений эмпирического и теоретического распределений не отвергается.
Условия применения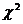 
:
1) число наблюдений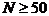 
;
2) частоты в интервалах больше 5 (в противном случае их объединяют). В нашем примере объединяем частоты 9-го и 10-го интервалов.
Критерий согласия Колмогорова (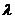
): 
| 
| 
|
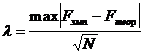
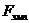
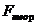
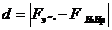
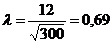. Если 
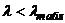с достаточно высокой степенью вероятности, гипотеза о соответствии эмпирического распределения нормальному не отвергается.
Практические задания
Date: 2015-07-27; view: 810; Нарушение авторских прав