
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Ранговые коэффициенты
|
|
2.1. Коэффициент 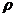 (Спирмэна)
(Спирмэна)
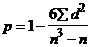
где d – ранговая разность;
n – число пар вариантов.
Варианты факторного признака х располагаются по возрастанию, затем проставляются ранги для вариантов результативного признака у (упорядочивание по одному из признаков обязательно при вычислении 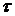 ).
).
В случае совпавших рангов вычисляются поправки Т и U:
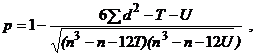
где 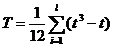 ,
, 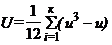
t, и – соответственно число единиц с совпавшим рангом в последовательностях (число совпадений)
l, k – число групп с совпавшими рангами в последовательностях.
2.2. Коэффициент 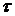 (Кендэла)
(Кендэла)

где S – сумма баллов. Баллом +1 оценивается пара рангов, имеющих по двум признакам одинаковый порядок, а баллом –1 – пара рангов с обратным порядком.
Для совпавших рангов вычисляются поправки Т и U, и расчетная формула принимает следующий вид:
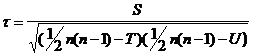
где 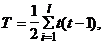
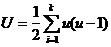
3. Коэффициенты взаимной сопряженности. Используются как показатели тесноты связи качественных или количественных признаков.
| 3.1. Коэффициент Пирсона | 3.2. Коэффициент Чупрова: | 3.3. Коэффициент Крамера |
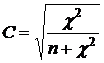
| 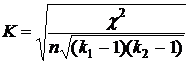
| 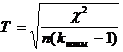 при
при 
|
где n – число наблюдений;
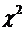 – критерий хи-квадрат наличия связи между признаками.
– критерий хи-квадрат наличия связи между признаками.
Расчетное значение 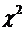 определяется по формуле:
определяется по формуле:
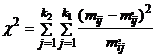 ,
,
где 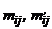 - соответственно эмпирические и теоретические частоты в i строке j-го столбца;
- соответственно эмпирические и теоретические частоты в i строке j-го столбца;
k1, k2 – соответственно число групп в строках и столбцах таблиц.
Вычисление 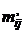 и критерия
и критерия 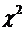 строится на основе анализа распределения частот в таблице сопряженности по строкам и столбцам. Если признак, положенный в основу группировки по строкам, не зависит от признака, положенного в основу группировки по графам, то в каждой строке распределение частот (условное распределение) должно быть пропорционально распределению их в итоговой строке (безусловное распределение). Такое распределение можно считать теоретическим, рассчитанным при предположении отсутствия зависимости между изучаемыми признаками. При независимости признаков
строится на основе анализа распределения частот в таблице сопряженности по строкам и столбцам. Если признак, положенный в основу группировки по строкам, не зависит от признака, положенного в основу группировки по графам, то в каждой строке распределение частот (условное распределение) должно быть пропорционально распределению их в итоговой строке (безусловное распределение). Такое распределение можно считать теоретическим, рассчитанным при предположении отсутствия зависимости между изучаемыми признаками. При независимости признаков 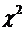 =0.
=0.
Проверка существенности связи осуществляется путем сравнения 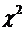 найденного с
найденного с 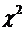 критическим при числе степеней свободы (k1–1)(k2–1) при выбранном уровне значимости
критическим при числе степеней свободы (k1–1)(k2–1) при выбранном уровне значимости 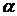 . (Проверяется гипотеза Но:
. (Проверяется гипотеза Но: 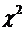 =0, когда условные распределения совпадают и, следовательно, признаки независимы).
=0, когда условные распределения совпадают и, следовательно, признаки независимы).
Пример: Измерение тесноты связи между двумя признаками: образование мужа и жены
Таблица 2
| Образование жены | ||||
| Образование мужа | неполное среднее | среднее | высшее и среднее специальное | Всего |
| Неполное среднее | 58 (20,5) | 36 (43,6) | 4 (34) | |
| [59,2] | [36,7] | [4,1] | ||
| Среднее | 30 (42,2) | 122 (89,9) | 50 (70) | |
| [14,9] | [60,4] | [24,7] | ||
| Высшее и среднее специальное | 6 (31,3) | 42 (66,6) | 102 (52,1) | |
| Условное распределение, в % | [4] | [28] | [68] | |
| Всего | ||||
| Безусловное распределение, в % | [20,9] | [44,4] | [34,7] | 100 |
| Решение |
В таблице 2 в круглых скобках показаны теоретические частоты:
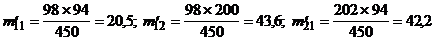
Расчетное значение критерия:


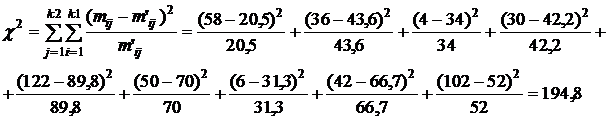
По таблицам математической статистики для уровня значимости 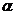 = 0,05, при числе степеней свободы (3–1)(3–1) = 4 табличные значения
= 0,05, при числе степеней свободы (3–1)(3–1) = 4 табличные значения 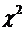 =9,5 (см. таблицу 3), т.е.
=9,5 (см. таблицу 3), т.е. 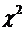 расч.>
расч.> 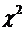 табл., следовательно, гипотеза об отсутствии зависимости между уровнями образования мужа и жены отвергается.
табл., следовательно, гипотеза об отсутствии зависимости между уровнями образования мужа и жены отвергается.
Величина 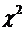 зависит от объема совокупности и поэтому не характеризует степень тесноты связи.
зависит от объема совокупности и поэтому не характеризует степень тесноты связи.
Таблица 3
Критические значения критерия 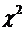
Значение 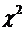 , превышающего табличное, при
, превышающего табличное, при 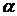 =0,05
=0,05
 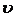 
| 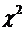
| 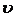
| 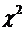
| 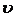
| 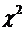
|
| 3,84 | 19,68 | 32,67 | |||
| 5,99 | 21,03 | 33,92 | |||
| 7,81 | 22,36 | 35,17 | |||
| 9,49 | 23,68 | 36,42 | |||
| 11,07 | 25,00 | 37,65 | |||
| 12,59 | 26,30 | 38,89 | |||
| 14,07 | 27,59 | 40,11 | |||
| 15,51 | 28,87 | 41,34 | |||
| 16,62 | 30,14 | 42,56 | |||
| 18,31 | 31,41 | 43,77 |
Коэффициент сопряженности Пирсона:
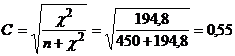
Полученное значение свидетельствует о наличии умеренной степени тесноты связи между признаками. (Поскольку при независимости признаков 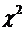 =0, то С = 0).
=0, то С = 0).
Коэффициент сопряженности Чупрова:
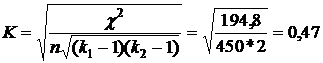
Данный результат подтверждает наличие умеренной связи между признаками.
Date: 2015-07-27; view: 521; Нарушение авторских прав