
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ
|
|
Регрессионными называются такие связи, когда при одном и том же значении признака Х встречаются разные значения признака У, при этом между ними имеется такое соотношение, что определенному изменению признака Х соответствуют средние изменения признака У. Следовательно, это связь, проявляющаяся в общем, в среднем, во всей совокупности явлений в целом. Такого рода связи характеризуются нежесткими соотношениями между переменными, их множественностью.
Корреляционные связи бывают прямолинейные и нелинейные. Для выражения связи между двумя признаками подбирают наиболее подходящие из известных
математических уравнений, функций (прямую, параболу, гиперболу и т.д.). Уравнение прямой имеет следующий вид:
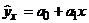 .
.
Применительно к измерению связей здесь У представляет собой результативный признак, Х – факторный признак, а0 и а1 – параметры прямой, а само уравнение называется уравнением регрессии.
Нахождение этих параметров производится на основе выравнивания по способу наименьших квадратов, которые приводят к системе двух линейных уравнений с двумя неизвестными:
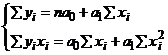
Решая это уравнение способом определителей, находим:
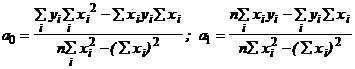 ;
;
или разделив первое уравнение на n, получим: 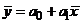 , откуда
, откуда 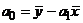 .
.
Найдем параметры а0 и а1 и запишем уравнение связи между балансовой прибылью (БП) и капиталом (К) десяти коммерческих банков.
Таблица 4
| Банк | БП (yi) | К (хi) | xiyi | 
| 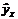
| 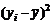
| 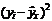
| Ранги | d2=(Ry-Rx)2 | |
| № п/п | млрд. руб. | млрд. руб. | RY | RX | ||||||
| А | ||||||||||
| 1. | 19,2 | 129,5 | 2486,4 | 16770,25 | 53,7 | 2,53 | 1186,80 | |||
| 2. | 46,0 | 46,3 | 2129,8 | 2143,69 | 19,9 | 635,54 | 681,21 | |||
| 3. | 93,8 | 152,6 | 14313,88 | 23286,76 | 63,0 | 5330,46 | 946,79 | |||
| 4. | 12,6 | 18,4 | 231,84 | 338,56 | 8,6 | 67,08 | 16,16 | |||
| 5. | 16,3 | 12,8 | 208,64 | 163,84 | 6,3 | 20,16 | 99,80 | |||
| 6. | 6,1 | 56,7 | 345,87 | 3214,89 | 24,1 | 215,8 | 324,72 | |||
| 7. | 5,4 | 13,8 | 74,52 | 190,44 | 6,7 | 236,85 | 1,72 | |||
| 8. | 3,4 | 4,5 | 15,3 | 20,25 | 2,9 | 302,41 | 0,21 | |||
| 9. | 3,0 | 11,5 | 34,5 | 132,25 | 5,8 | 316,48 | 7,73 | |||
| 10. | 2,1 | 38,9 | 81,69 | 1513,21 | 16,9 | 349,32 | 219,04 | |||
| Итого | 207,9 | 19922,44 | 47774,14 | 207,9 | 7476,626 | 3484,18 |
Продолжение таблицы 4
| Знаки отклонений | |||||||||||
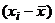
| + | – | + | – | – | + | – | – | – | – | |
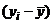
| – | + | + | – | – | – | – | – | – | – | |
| C или Н | Н | Н | С | С | С | Н | С | С | С | С |
Отсюда, 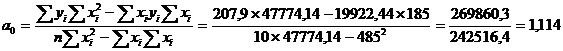
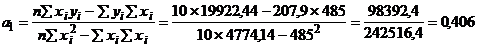
Следовательно, уравнение связи между капиталом и балансовой прибылью 10 банков будет: 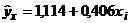 . Оно означает, что с увеличением капитала на 1 рубль балансовая прибыль в среднем вырастет на 40,6 копеек. Подставив в это уравнение конкретные значения х, находим для всех 10 банков
. Оно означает, что с увеличением капитала на 1 рубль балансовая прибыль в среднем вырастет на 40,6 копеек. Подставив в это уравнение конкретные значения х, находим для всех 10 банков 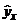 , т.е. теоретическое значение прибыли. Для расчета корреляционного отношения рассчитываем общую дисперсию У и остаточную дисперсию:
, т.е. теоретическое значение прибыли. Для расчета корреляционного отношения рассчитываем общую дисперсию У и остаточную дисперсию:

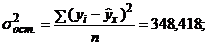
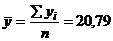 .
.
Корреляционное отношение:
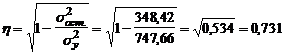 ,
,
что свидетельствует о наличии связи между признаками.
Подставив в формулу корреляционного отношения: 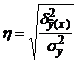 , где
, где 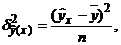
вместо 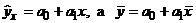 получим:
получим:
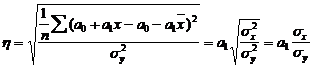 ,
,
т.е. для линейной зависимости 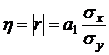
Если в формуле 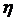 для линейной зависимости подставить значение а1, выраженное из системы уравнений, получим линейный коэффициент корреляции Пирсона:
для линейной зависимости подставить значение а1, выраженное из системы уравнений, получим линейный коэффициент корреляции Пирсона:
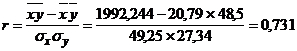 ,
,
где 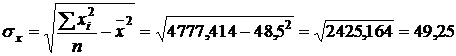 ,
,
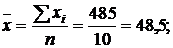
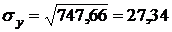
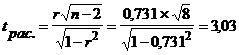 ;
; 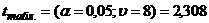
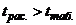 , следовательно Но:
, следовательно Но: 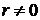 .
.
Ранговые показатели тесноты связи: p Спирмэна, 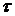 Кэндэла.
Кэндэла.
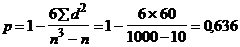 ,
, 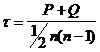
Прежде чем найти Р и Q, следует упорядочить ранги по одному из признаков, например, у. Тогда ряд рангов будет иметь вид:
| № п/п | Ry | Rx | P | (–) Q |
| 1. | ||||
| 2. | ||||
| 3. | ||||
| 4. | ||||
| 5. | ||||
| 6. | ||||
| 7. | ||||
| 8. | ||||
| 9. | ||||
| 10. | – | – | ||
| Итого |
Р – количество наблюдений, ранг которых больше данного;
Q – количество наблюдений, ранг которых меньше данного. Данное значение отражает число нарушений последовательности рангов, поэтому Q записывается со знаком “–”;
n – число наблюдений;
1/2´n(n–1) – общее число сравнений, т.е. максимальная величина (P+Q).
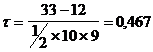
Коэффициенты р и 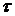 подтверждают наличие умеренной связи между величиной капитала и балансовой прибылью банков.
подтверждают наличие умеренной связи между величиной капитала и балансовой прибылью банков.
Коэффициент Фехнера (1887 г.): 
где С и H – соответственно число пар совпадающих и несовпадающих знаков отклонений значений признаков х и у от своего среднего значения 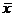 и
и 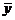 (cм. гр.11–13).
(cм. гр.11–13).
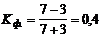
Проверка статистической значимости коэффициента корреляции (r).
1. Рассчитывается величина t (как отношение r к его ошибке)
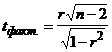 ,
,
где n – число наблюдений; (n –2) – число степеней свободы.
2. По таблице распределения Стьюдента (n 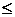 30) находится пороговое значение tтабл., соответствующее заданному уровню значимости
30) находится пороговое значение tтабл., соответствующее заданному уровню значимости 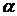 (
(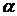 =0,05 или
=0,05 или 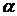 =0,02) и числу степеней свободы.
=0,02) и числу степеней свободы.
3. Если tф.>tт, коэффициент корреляции признается статистически значимым при уровне значимости 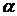 .
.
| v | Вероятность 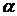 =St(t)=P(|T|)>tтабл. =St(t)=P(|T|)>tтабл.
| ||||||||||||
| 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0,4 | 0,3 | 0,2 | 0,1 | 0,05 | 0,02 | 0,01 | 0,001 | |
| 0,158 | 0,325 | 0,51 | 0,727 | 1,376 | 1,963 | 3,078 | 6,314 | 12,706 | 31,821 | 63,656 | 636,61 | ||
| 0,142 | 0,289 | 0,445 | 0,617 | 0,816 | 1,061 | 1,386 | 1,886 | 2,92 | 4,303 | 6,965 | 9,925 | 31,598 | |
| 0,137 | 0,277 | 0,424 | 0,584 | 0,765 | 0,978 | 1,25 | 1,638 | 2,353 | 3,182 | 4,541 | 5,841 | 12,941 | |
| 0,134 | 0,271 | 0,414 | 0,569 | 0,741 | 0,941 | 1,19 | 1,533 | 2,132 | 2,776 | 3,747 | 4,604 | 8,61 | |
| 0,132 | 0,267 | 0,408 | 0,559 | 0,727 | 0,92 | 1,156 | 1,476 | 2,015 | 2,571 | 3,365 | 4,043 | 6,859 | |
| 0,131 | 0,265 | 0,404 | 0,553 | 0,718 | 0,906 | 1,134 | 1,44 | 1,943 | 2,447 | 3,143 | 3,707 | 5,959 | |
| 0,13 | 0,263 | 0,402 | 0,549 | 0,711 | 0,896 | 1,119 | 1,415 | 1,895 | 2,365 | 2,998 | 3,499 | 5,405 | |
| 0,13 | 0,262 | 0,399 | 0,546 | 0,706 | 0,889 | 1,18 | 1,397 | 1,89 | 2,306 | 2,896 | 3,355 | 5,041 | |
| 0,129 | 0,261 | 0,398 | 0,543 | 0,703 | 0,883 | 1,1 | 1,383 | 1,883 | 2,262 | 2,821 | 3,25 | 4,781 | |
| 0,129 | 0,26 | 0,327 | 0,452 | 0,7 | 0,879 | 1,093 | 1,372 | 1,812 | 2,228 | 2,764 | 3,169 | 4,583 | |
| 0,129 | 0,26 | 0,396 | 0,54 | 0,697 | 0,876 | 1,088 | 1,363 | 1,796 | 2,201 | 2,718 | 3,106 | 4,437 | |
| 0,128 | 0,259 | 0,395 | 0,539 | 0,695 | 0,873 | 1,083 | 1,356 | 1,782 | 2,179 | 2,681 | 3,055 | 4,318 | |
| 0,128 | 0,259 | 0,394 | 0,538 | 0,694 | 0,87 | 1,079 | 1,35 | 1,771 | 2,16 | 2,65 | 3,012 | 4,221 | |
| 0,128 | 0,258 | 0,393 | 0,537 | 0,692 | 0,868 | 1,076 | 1,345 | 1,761 | 2,145 | 2,624 | 2,977 | 4,14 | |
| 0,128 | 0,258 | 0,393 | 0,536 | 0,691 | 0,866 | 1,074 | 1,341 | 1,753 | 2,131 | 2,602 | 2,947 | 4,073 | |
| 0,128 | 0,258 | 0,392 | 0,535 | 0,69 | 0,865 | 1,071 | 1,337 | 1,746 | 2,12 | 2,583 | 2,921 | 4,015 | |
| 0,128 | 0,257 | 0,392 | 0,534 | 0,689 | 0,863 | 1,069 | 1,333 | 1,74 | 2,11 | 2,567 | 2,898 | 3,965 | |
| 0,127 | 0,257 | 0,392 | 0,534 | 0,688 | 0,862 | 1,067 | 1,33 | 1,734 | 2,101 | 2,552 | 2,876 | 3,922 | |
| 0,127 | 0,257 | 0,391 | 0,533 | 0,688 | 0,861 | 1,066 | 1,328 | 1,729 | 2,093 | 2,539 | 2,861 | 3,833 | |
| 0,127 | 0,257 | 0,391 | 0,533 | 0,687 | 0,86 | 1,064 | 1,325 | 1,725 | 2,086 | 2,528 | 2,845 | 3,85 |
Практические задания
Date: 2015-07-27; view: 571; Нарушение авторских прав