Постановка задачи обработки результатов измерений. Вероятностная постановка обработки результатов измерений

Построение законов распределения СВпо опытным данным. Основные теоремы теории вероятности. Формы законов распределения СВ. Функция распределения. Плотность распределения. Числовые характеристики СВ. Алгоритм вычисления числовых характеристик СВ.

Приближением функции распределения случайной величины является эмпирическая функция распределения:
F'(x) = \sum_{i=1}^n [x <= x_i] / n.

Основные теоремы теории вероятности:
1) ЗБЧ:
Пусть есть бесконечная последовательность независимых одинаково распределённых случайных величин x_i. Тогда
\sum_{i=1}^n x_i / n ->Ex почти наверное, где Ex - математическое ожидание x_i.
2) ЦПТ:
Пусть есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию. Тогда
(\sum_{i=1}^n x_i - Ex * n) / \sqrt(Dx * n) -> N(0, 1) по распределению, где Ex и Dx - математическое ожидание и дисперсия x_i соответственно.

Функцией распределения данной случайной величины x называется функция
F(u) = P(u < x).

Распределения рассматриваются дискретные и абсолютно непрерывные.
Первые характеризуются счетным числом исходов ненулевой вероятности, а вторые - функцией распределения, имеющей плотность.
Плотностью случайной величины x с функцией распределения F(u) называется всякая такая функция f, такая что
F(u) = int_{-\infty}^u f(t) dt.

Числовые характеристики случайной величины - это ее моменты. Моментом порядка k называется интеграл
\int{-\infty}^{\infty} t^k f(t) dt.
Первый момент называется математическим ожиданием.
Разность второго момента и квадрата первого момента называется дисперсией.

По сути, вычисление k-ого момента - это вычисление интеграла.

6. Одномерный, двумерный нормальный закон распределения СВ и их параметры.

7. Интеграл вероятности и его приближение.

8. Генераторы случайных чисел. Псевдослучайные числа, их характеристики и способы их моделирования на ЭВМ.

10. Определение длины периода и отрезка апериодичности.

11. Проверка датчиков на случайность.

12. Проверка датчиков на равномерность.

13. Проверка датчиков на коррелированность.

14. Проверка датчиков путём решения контрольной задачи(вычисление числа ПИ).

16. Методы вычисления кратных интегралов методом статистических испытаний: 1) по математическому ожиданию; 2) по вероятности. Сведение решения задачи стрельбы к вычислению кратных интегралов.

Вопросы:
1. Вычисление одинарного интеграла методом статистических испытаний по математическому ожиданию.
2. Вычисление одинарного интеграла методом статистических испытаний по вероятности.
Поскольку интегралы малого порядка кратности вычисляются другими, более точными методами, данные примеры используются для иллюстрации идеи применения метода статистических испытаний для вычисления кратных интегралов. На занятии преподаватель показывает, как обобщается данная методика для вычисления кратных интегралов. Дается сравнительная оценка трудоемкости двух излагаемых методов. Показывается метода вычисления интеграла по математическому ожиданию в сравнении с вычислением интеграла по вероятности. Далее студентам для самостоятельного решения предлагается задача. Рассматриваются несколько приемов решения данной задачи методом статистических испытаний. Для лучшего усвоения излагаемого материала целесообразно представлять решение задачи в следующем порядке:
а) на первом этапе составляется последовательность вычислений;
б) на втором этапе по составленной последовательности вычислений записывается алгоритм решения задачи на алгоритмическом языке Паскаль.

ВЕЗДЕ ИНТЕГРИРОВАНИЕ ИДЕТ ПО СИГМА!
III. Учебные материалы

1. Методы вычисления кратных интегралов.
а) по математическому ожиданию: Пусть требуется вычислить
I=INT INT... INT PHI(x1,...,xN)dxdx...dx
где PHI(x1,x2,...,xm) - непрерывна в ограниченной замкнутой области S, при этом
ai
Интеграл преобразуется так, чтобы новая область интегрирования s была расположена внутри единичного m-мерного куба. Произведя замену переменных
xi = ai + (bi - ai) KSIi,
где KSIi - равномерно распределенные случайные числа из [0,1], будем иметь
I=ABS(J)*INT INT... INT PHI[a1+(b1-a1) KSI1,..., am+(bm-am) KSIm] dKSI 1dKSI2... dKSIm,
где |J |= П(bi-ai)
Преобразуем интеграл к виду:
I=ABS(J)*INT INT … INT dx1dx2... dxm *INT INT … INT (1/(INT INT … INT dKSI1 … dKSIm)*PHI[…]dKSI1…dKSIm)

Пустьв m-мерныйединичныйкубслучайноиравномернобросаетсяточкаМ(x1,...,xm), тогда
I = | J | P{M(KSI1,...,KSIm) }*M[PHI (M(KSI1,...,KSIm)) ].
Если в n случаях из N точка Mi, i = 1,2,...,N, то
I=ABS(J)*n/N*1/n*SUMMAPHI(Mi) или I=ABS(J)*SUMMAPHI(Mi)

б) по вероятности
В этом случае определяются экстремальные значения подинтегральной функции:
PHImin Интеграл преобразуется так, чтобы область интегрирования и подинтегральная функция была расположена внутри единичного (m+1) - мерного куба. Произведя замену переменных xi = ai + (bi - ai)KSIi, (i = 1,2,...,m), а также, введя новую подинтегральную функцию PHI*:
PHI(x1,x2,...,xm)= PHImin + (PHImax - PHImin)PHI*,
где KSIi - случайные числа, равномерно распределенные в [0,1] 0 < PHI* < 1.
Будемиметь
I = ABS(J)**(PHImax - PHImin)**INT INT … INT PHI* (KSI1,...,KSIm) dKSI1...dKSIm +
+ ABS(J)**PHImin**INT INT … INT dKSI1...dKSIm

В (m+1)-мерный единичный куб N раз бросается случайная точка Mi(KSI1i,...,KSImi) и каждый раз проверяется условие: Mi, и Mi V, где V - область, расположенная внутри единичного (m+1) - мерного куба, ограниченная кривой PHI*(KSI1,...,KSIm). Условие Mi V эквивалентно выполнению условий: Mi и
PHImin + (PHImax - PHImin)KSIm+1i Пусть в n1 случаях из N выполняется условие Mi V, а в n2 случаях из N выполняется условие Mi. Тогда:
I=ABS(J)*[(PHImax-PHImin)*n1/N+PHImin*N2/b]

2. Cведение решения задач стрельбы к вычислению кратных интегралов.

Задача. Объект, подвергающийся бомбардировке, будет поражен, если разрыв произойдет на расстоянии R от объекта. Известны систематические и случайные ошибки бомбометания. Определить вероятность поражения объекта.
Решение: Искомая вероятность определяется по формуле:


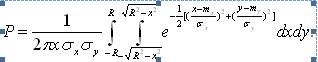
Постановка задачи обработки результатов измерений. Вероятностная постановка обработки результатов измерений.

1. Постановка задачи обработки результатовизмерений

Рассмотрим некоторый математический аппарат, применяемыйпри формализации и автоматизации процессов вторичной обработки АСУ ПВО. Этопродемонстрируем на примере операций сглаживания и экстраполяции координат приавтосопровождении цели.
Постановказадачи.
Составить алгоритм для обработки nравноотстоящих по времени измерений Х₁,Х₂,...,Х_п (под X понимаетсялибоизмеренная дальность до цели, либо угол места, либо азимут цели, и т.д.).Интервал измеренийDt.
Впроцессе обработки измерений сформировать массив Y, содержащий сглаженныезначениякоординат цели Xy(t) =x_c(t),
m производных у^(l) =х_c^(l),l = 1,...т и экстраполированное значение у_э (t) = х_с (t_s+l). Составить так жепрограмму расчета коэффициентов для сглаживания, численногодифференцированияи экстраполяции результатов измерений.
Сглаживаниепроизводится последовательно по s точкам.
Исходныеданные:
s - количество измерений,
т - степеньсглаживающего полинома,
k(1 £k£s) - номер измерения, для которого вычисляютсяпараметры сглаженной функции,
DХ - допустимая величинаотклонения измеренного значения от сглаженного (строб). (Величина доверительного интервала, в пределахкоторого с заданной вероятностью наблюдается отклонение измерения от сглаживающей функции).
Грубымизмерением X(t) считатьтоизмерение,котороеневошловстроб,т.е. |x(t_s+1)-x_c(t_s+1)| >D Х, тогда в местоизмеренного берется экстраполированное. Если наблюдается подряд 3 грубыхизмерения, производится остановка программы.