Свойства и методы расчета показателей вариации

Средние величины раскрывают важную обобщающую характе­ристику совокупности по варьирующему признаку. Рассчитав их, необходимо уяснить, насколько они показательны, типичны или однородны. Для этого необходимо определить показатели вариации признака. Простейшей из таких характеристик может служить размах вариации, который вычисляется как разность между наибольшим и наименьшим значениями признака:

.

Размах вариации показывает только крайние отклонения, но не отражает отклонений от средней всех значений признака в вариационном ряду. Последнее можно по­лучить, если рассчитать отклонения всех вариант от средней 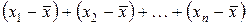и вычислить среднюю арифмети­ческую из всех отклонений.

Известно, что сумма всех положительных (которые больше средней) и всех отрицательных (которые меньше средней) отклонений равна нулю. Поэтому при расчете средней арифметической из отклонений необходимо абстрагироваться от знаков «+» и «-». В этом случае сумма отклонений 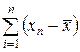, разделенная на число отклонений 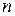, а при наличии частот - на число 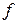, и будет сред­ним арифметическим отклонением. В связи с этим расчетная формула будет выглядеть следующим образом:

.

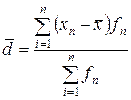В результате мы получили среднее арифметическое (линейное) от­клонение, которое обозначается символом 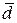. Это вторая мера измере­ния вариации признака.

Среднее арифметическое (линейное) отклонение в статистиче­ском анализе применяется редко. Обычно используют третий показа­тель вариации — дисперсию, или средний квадрат отклонений. Она обо­значается символом 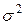(сигма малая в квадрате) и представляет собой то же среднее арифметическое отклонение 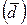, но только отклонения возведены в квадрат, и из квадратов отклонений вычисляют среднюю величину:

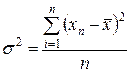, а при наличии частот .

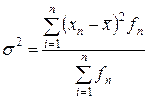При расчете дисперсии не надо абстрагироваться от знаков (+ и -) отклонений, так как при возведении в квадрат все знаки отклонений становятся положительными.

Если извлечь корень квадратный из дисперсии, то мы получим сле­дующий, четвертый, показатель вариации — среднее квадратическое от­клонение, которое обозначается символом а (сигма малая):

Дисперсия и среднее квадратическое отклонение являются наиболее распространенными и общепринятыми показателями вариации изучаемо­го признака.

В юридической статистике они используются при сравнительных статистических исследованиях, для обоснования ошибки репрезента­тивности (ошибки выборки) выборочного наблюдения, а также при изучении корреляционных и иных статистических связей между факторными при­знаками и результативными, или между причиной и следствием.

Дисперсия и среднее квадратическое отклонение обладают рядом свойств, которые приводятся без доказательств:

1) дисперсия постоянной величины равна нулю;

2) дисперсия не меняется, если все варианты увеличить или умень­шить на какое-то постоянное число А;

3) если все варианты умножить на какое-то постоянное число А, то дисперсия увеличится в А² раз, а среднее квадратическое отклонение - в А раз;

4) если все варианты разделить на какое-то постоянное А, то диспер­сия уменьшится в А² раз, а среднее квадратическое отклонение - в А раз.

Эти и другие свойства дисперсии могут быть использованы для уп­рощения и оптимизации техники расчетов.

Пятый (по счету) показатель вариации - это коэффициент вариа­ции. В отличие от размаха вариации, среднего линейного, среднего квадратического отклонения и дисперсии, которые выражаются в аб­солютных и именованных числах, коэффициент вариации является показателем относительным. Он выражается в процентах, обозначает­ся символом V и рассчитывается по формуле:

,

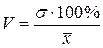где V— коэффициент вариации; 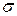- среднее квадратическое отклонение; 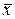- средний арифметический показатель.

Коэффициент вариации предоставляет большие возможности для сравнительных изучений, поскольку сравнивать, например, средние квадратические отклонения вариационных рядов с разными уровнями непосредственно нельзя. Коэффициент вариации в известной мере яв­ляется критерием типичности средней. Если он относительно боль­шой (например, выше 40%), то это значит, что типичность такой сред­ней очень невысока. И наоборот, если его значение малое, то средняя является типической и надежной.

Date: 2015-07-27; view: 565; Нарушение авторских прав