Виды средних и особенности их расчета

Структурные средние величины

В качестве структурных средних чаще всего используют показатели моды – наиболее часто повторяющегося значения признака – и медианы – величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части.

Мода – величина признака, которая чаще всего встречается в данной совокупности. Применительно к вариационному ряду модой является наиболее часто встречающееся значение ранжированного ряда. Она показывает размер признака, свойственный значи–тельной части совокупности, и определяется по фор–муле:

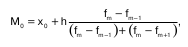
где х0 – нижняя граница интервала;

h – величина интервала;

fm – частота интервала;

fm-1 – частота предшествующего интервала;

fm+1 – частота следующего интервала.

Медианой называется вариант, расположенный в центре ранжированного ряда. Медиана делит ряд на две равные части таким образом, что по обе стороны от нее находится одинаковое количество единиц со–вокупности. При этом у одной половины единиц сово–купности значение варьирующего признака меньше ме–дианы, у другой – больше.

Описательный характер медианы проявляется в том, что она характеризует количественную границу значений варьирующего признака, которыми облада–ет половина единиц совокупности.

При определении медианы в интервальных ва–риационных рядах сначала определяется интервал, в котором она находится (медианный интервал). Этот интервал характерен тем, что его накопленная сумма частот равна или превышает полусумму всех ча–стот ряда. Расчет медианы интервального ва–риационного ряда производится по формуле:

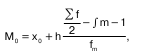
где х0 – нижняя граница интервала;

h – величина интервала;

fm – частота интервала;

f – число членов ряда;

?m- 1 – сумма накопленных членов ряда, предше–ствующих данному.

Наряду с медианой для более полной характери–стики структуры изучаемой совокупности применяют и другие значения вариантов, занимающих в ранжи–рованном ряду вполне определенное положение. К ним относятся квартили и децили. Квартили делят ряд по сумме частот на четыре равные части, а деци-ли – на десять равных частей. Квартилей насчитыва–ется три, а децилей – девять.

Медиана и мода в отличие от средней арифмети–ческой не погашают индивидуальных различий в зна–чениях варьирующего признака и поэтому являются дополнительными и очень важными характеристика–ми статистической совокупности. На практике они ча–сто используются вместо средней либо наряду с ней. Особенно целесообразно вычислять медиану и моду в тех случаях, когда изучаемая совокупность содер–жит некоторое количество единиц с очень большим или очень малым значением варьирующего признака.

Степенные средние величины

Степенные средние величины получили свое название по виду функции, используемой для их расчета.
Если значения признаков в статистической совокупности не повторяются, степенную среднюю величину вычисляют в простой форме - это простая степенная средняя, при повторяющихся значениях – во взвешенной форме. Количество повторяющихся значений одного и того же признака (Х i) называется его весом (f i).

Простая степенная средняя величина рассчитывается по формуле
, (6.1)

где k – показатель степени средней величины.

При k = - 1 по данной формуле рассчитывают гармоническую среднюю величину (Х гарм.).
Если 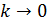, на основе теории пределов по данной формуле определяют геометрическую среднюю величину (Х геом.).

Далее при k = 1 находят арифметическую среднюю, при k = 2 - квадратическую, при k = 3 - кубическую, при k = 4 - биквадратическую и т.д.

Если одно и то же значение признака встречается несколько раз, рассчитывают взвешенную среднюю величину:

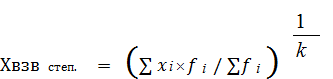, (6.2)
где f i - это вес (частота значений признака xi).

Гармоническая средняя применяется если:
1) осредняемый признак является мерой времени и выражен в секундах и минутах.
2) осредняемая величина задана в виде функции неявного вида.
, (6.3)
где n – количество единиц в совокупности.

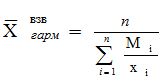, (6.4)
где ,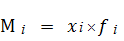
Геометрическая средняя применяется при нахождении средних темпов или коэффициентов роста, т. к. она показывает во сколько раз в среднем одна величина в упорядоченной совокупности больше (или меньше) другой.
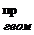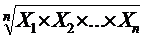= , (6.5)
где n – число сомножителей (осредняемых значений признака).
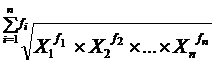= (6.6)
Арифметическая средняя определяется по формулам:
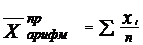(6.7)
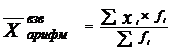(6.8)
Квадратическая средняя используется в тех случаях, когда осредняемая величина x задана в виде квадратической функции.
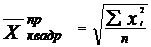(6.9)
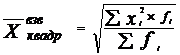(6.10)
Кубическая средняя применяется, если осредняемая величина задана в виде квадратической функции.
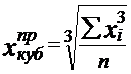(6.11)
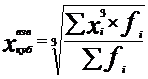(6.12)
Биквадратическая средняя рассчитывается как степенная средняя четвертого порядка и применяется при осреднении признака, являющегося функцией четвертого порядка.

Date: 2015-07-27; view: 514; Нарушение авторских прав