Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Решение. 1) Экономико-математическая модель исходной задачи
|
|
1) Экономико-математическая модель исходной задачи.
Xi – объем выпускаемой продукции на i-м филиале предприятия.
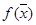= 83X1+89X2+95X3+98X4 -> min,
Ограничения
X1+X2+X3+X4 ³ 300 (тыс. штук)
120X1+80X2+50X3+40X4 £ 18 (млн.руб.),
X1,2,3,4 ³ 0.
| Y1 | |||||
| Y2 |
Экономико-математическая модель двойственной задачи.
Y1 – двойственная оценка выпускаемой продукции, которая может быть ценой изделия;
Y2 – двойственная оценка капитальных вложений, которая может быть представлена как коэффициент эффективности капитальных вложений.
g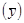 
= 300000 Y1+18000000 Y2 -> mах
1 Y1+120Y2 £ 83
1 Y1+ 80Y2 £ 89
1 Y1+ 50Y2 £ 95
1 Y1+ 40Y2 £ 98
2) для определения оптимального плана двойственной задачи воспользуемся соотношениями второй теоремы двойственности. Если какое-либо ограничение исходной задачи выполняется как строгое неравенство, то соответствующая двойственная оценка равна нулю
(
).
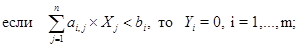0+100000+200000+0 = 300000
120´0+80´100000+50´200000+4´0 = 18000000
Если какая-либо переменная исходной задачи входит в оптимальный план, то соответствующее ограничение двойственной задачи выполняется как строгое равенство
).
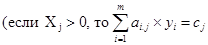В нашей задаче Х2 =100000>0 и Х3 =200000>0, поэтому второе и третье ограничения двойственной задачи обращаются в уравнения, решая которые найдем Y1 и Y2.
1Y1 + 50Y2 = 95 Y1= 105 – средняя цена изделия
1Y1 + 80Y2 = 89 Y2= –0.2 – двойственная оценка капитальных вложений.
105 =95 +50´0.2 = 105
105 =89+ 80´0.2 = 105
На втором и третьем филиалах выпускать новые изделия целесообразно так как затраты на его освоение и выпуск не превышают цену изделия.
Проверим выполнение первой теоремы двойственности.
g 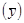= 300000Y1+18000000Y2=300000´105+18000000´(–0.2) = 279000000
= 83X1+89X2+95X3+98X4 = 83´0+89´100000+95´200000+98´0 = 279000000.
Полученные оптимальные планы говорят о том, что в первом и четвертом филиалах размещать заказы по выпуску новых изделий невыгодно (Х 1=0 и Х 4=0), так как затраты на производство единицы изделия в этих филиалах больше цены изделия.
1 ´Y1+ 120´Y2 = 83 Y1= 105 105+ 120´(-0.2) < 95 105< 95+24 = 119
1 ´Y1+ 40´Y2 = 98 Y2 = – 0.2 105+ 40´(-0.2) < 89 105<98+8 = 106.
Date: 2015-07-25; view: 475; Нарушение авторских прав