Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Сформулируем экономико-математическую модель задачи
|
|
Введем следующие обозначения: х1 – число женских костюмов; x2 – число мужских костюмов.
Прибыль от реализации женских костюмов составляет 10х 1, а от реализации мужских 20х 2, т.е. необходимо максимизировать целевую функцию
f(x) = 10´ х1 + 20´ х2 -> max.
Ограничения задачи имеют вид:
х1 + х2 £ 150 – ограничение по труду
2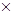 
х1 + 0.5 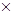х2 £ 240 – ограничение по лавсану
х1 + 3.5 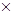х2 £ 350 – ограничение по шерсти
х2 ³ 60 – ограничение по костюмам
х1 ³ 0
Решение.
1. Указать адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки).
Обозначьте через Х1, Х2 количество костюмов каждого типа.В нашей задаче оптимальные значения вектора Х =(Х1, Х2,) будут помещены в ячейках A2:B2, оптимальное значение целевой функции в ячейке C3.
2. Ввести исходные данные.
Введите исходные данные задачи, как показано на рис.1.
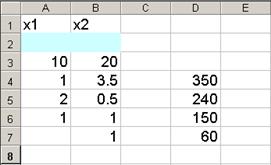
Рис. 1.
3. Ввести зависимость для целевой функции
• Курсор в ячейку "С3".
•Курсор на кнопку "Мастер функций", расположенную на панели инструментов.
• М1. На экране появляется диалоговое окно "Мастер функций шаг 1 из 2"
• Курсор в окно "Категория" накатегорию "Математические".
• Курсор в окно "Функции" на "СУММПРОИЗВ" (рис.2).
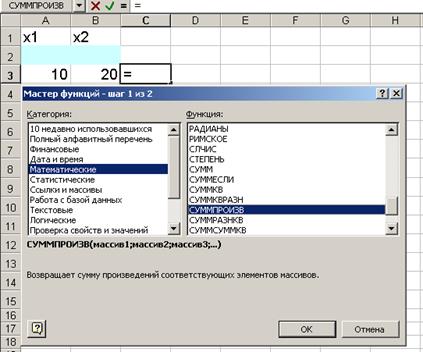
Рис 2.
На экране появляется диалоговое окно "СУММПРОИЗВ" (рис. 3)
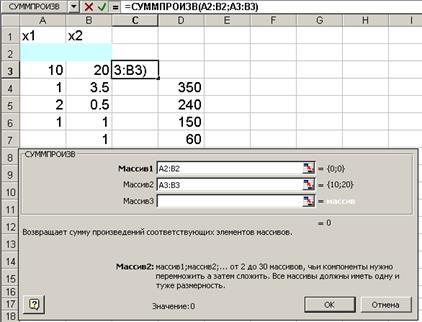
Рис. 3.
• В строку "Массив 1" [1] ввести А2:В2
• В строку "Массив 2" ввести А3:В3.
Массив 1 будет использоваться при вводе зависимостей для ограничений, поэтому на этот массив надо сделать абсолютную ссылку[2].
На экране: в ячейку С3 введена функция (рис. 4).
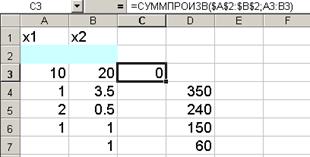
Рис. 4.
4. Ввести зависимости для ограничений.
• Курсор в ячейку "С3".
• На панели инструментов кнопка "Копировать в буфер".
• Курсор в ячейку "С4".
• На панели инструментов кнопка "Вставить из буфера".
• Курсор в ячейку "С5".
• На панели инструментов кнопка "Вставить из буфера".
• Курсор в ячейку "С6".
• На панели инструментов кнопка "Вставить из буфера".
• Курсор в ячейку "С7".
• На панели инструментов кнопка "Вставить из буфера".
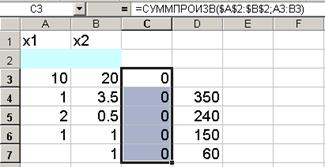
Рис.5.
Примечание. Содержимое ячеек С4 – С7 необходимо проверить. Они обязательно должны содержать информацию, как это показано для примера на рис.6 (в качестве примера представлено содержимое ячейки С5).
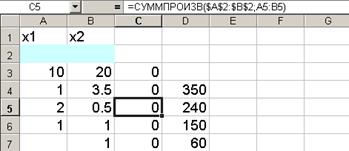
Рис. 6.
В строке "Меню" указатель мышки на имя "Сервис". В развернутом меню команда "Поиск решения". Появляется диалоговое окно "Поиск решения" (рис. 7).
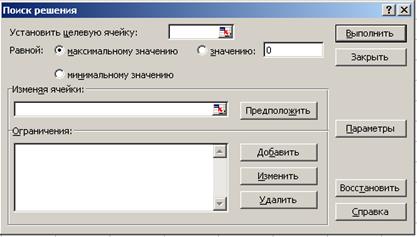
Рис. 7.
5. Назначить целевую функцию (установить целевую ячейку), указать адреса изменяемых ячеек.
• Курсор в строку "Установить целевую ячейку".
• Введите адрес ячейки "$С$3".
• Введите направление целевой функциив зависимости от условия вашей задачи: "Максимальному значению" ("Минимальному значению").
• Курсор в строку "Изменяя ячейки".
• Ввести адреса искомых переменных А$2:В$2. (Рис. 8.)
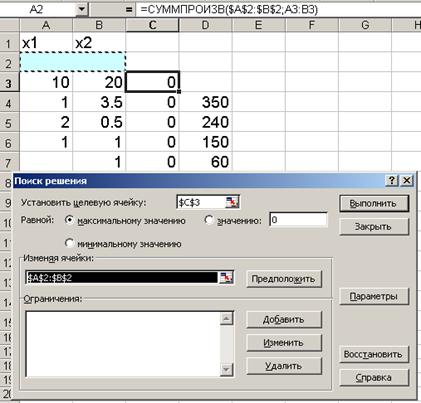
Рис. 8.
6. Ввести ограничения
• Указатель мышки на кнопку "Добавить". Появляется диалоговое окно "Добавление ограничения"
• В строке "Ссылка на ячейку" введите адрес $С$4.
• Ввести знак ограничения ≤.
• В строке "Ограничение" введите адрес $D$4 (рис. 9).
• Указатель мышки на кнопку "Добавить". На экране вновь диалоговое окно "Добавление ограничения" .
• Введите остальные ограничения задачи, по выше описанному алгоритму
• После введения последнего ограничения кнопка "ОК".
На экране появится диалоговое окно "Поиск решения" с введенными условиями (рис.10).
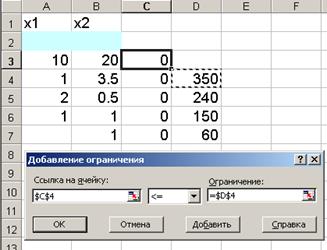
Рис. 9.
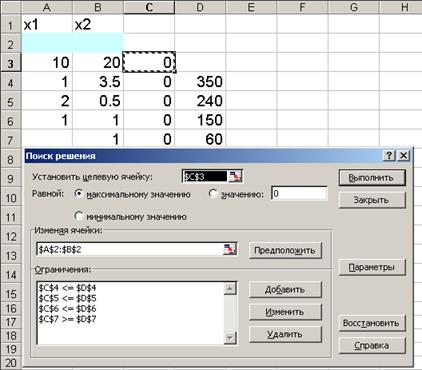
Рис.10
7. Ввести параметры для решения ЗЛП
• В диалоговом окне указатель мышки на кнопку "Параметры". На экране появляется диалоговое окно "Параметры поиска решения" (рис. 11).
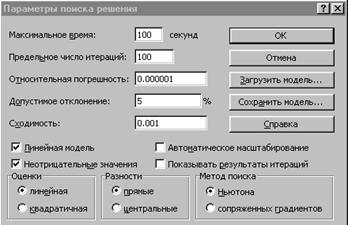
Рис.11
• Установите флажки в окнах "Линейная модель" (это обеспечит применение симплекс – метода) и "Неотрицательные значения".
• Указатель мышки на кнопку "ОК". На экране диалоговое окно "Поиск решения".
• Указатель мышки на кнопку "Выполнить".
Через непродолжительное время появится диалоговое окно "Результаты поиска решения" иисходная таблица с заполненными ячейками А3:В3 для значений Хi и ячейка С3 с максимальным значением целевой функции (рис.12).
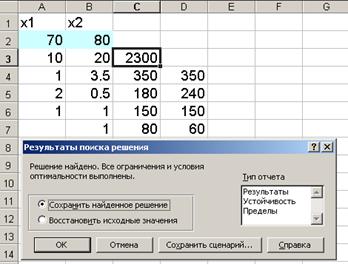
Рис.12
Если указать тип отчета "Устойчивость", то можно получить дополнительную информацию об оптимальном решении (Рис. 13).
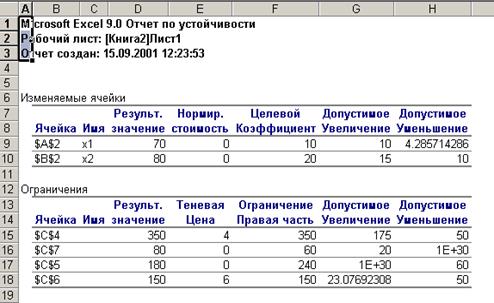
Рис. 13.
В результате решения задачи получили ответ:
Х1 = 70 – необходимо сшить женских костюмов,
Х2 = 80 – необходимо сшить мужских костюмов,
F(x) = 2300 что бы получить максимальную прибыль.
Решим еще одну задачу.
Задача 4. (Задача о коврах)
Фабрика имеет в своем распоряжении определенное количество ресурсов: рабочую силу, деньги, сырье, оборудование, производственные площади и т. п. Допустим, например, ресурсы трех видов рабочая сила, сырье и оборудование имеются в количестве соответственно 80 (чел/дней), 480(кг), 130 (станко/часов). Фабрика может выпускать ковры четырех видов. Информация о количестве единиц каждого ресурса необходимых для производства одного ковра каждоговида и доходах, получаемых предприятием от единицы каждого вида товаров, приведена в табл.1.
Таблица 1
| Ресурсы | Нормы расхода ресурсов на единицу изделия | Наличие ресурсов | |||
| Ковер А | Ковер В | Ковер С | Ковер D | ||
| Труд | |||||
| Сырье | |||||
| Оборудование | |||||
| Цена (тыс. руб.) |
Требуется найти такой план выпуска продукции, при котором общая стоимость продукции будет максимальная.
1. Сформулируем экономико – математическую модель задачи.
Обозначим через Х1, Х2, Х3, Х4 количество ковров каждого типа.
Целевая функция – это выражение, которое необходимо максимизировать
f(x) = 3Х1 +4Х2 +3Х3 +Х4
Ограничения по ресурсам
7Х1 +2Х2 +2Х3 +6Х4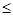 
80
5Х1 +8Х2 +4Х3 +3Х4 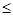480
2Х1 +4Х2 +Х3 +8Х4 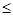130
Х1, Х2, Х3, Х4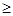 
0
Date: 2015-07-25; view: 562; Нарушение авторских прав