Модель задачи

Введем следующие обозначения: х₁ – число женских костюмов; x₂ – число мужских костюмов.

Прибыль от реализации женских костюмов составляет 10х₁, а от реализации мужских 20х₂, т.е. необходимо максимизировать целевую функцию

f(x) = 10´ х 1 + 20´ х 2 -> max

Ограничения задачи имеют вид:

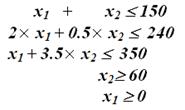
Первое ограничение по труду х₁ + х₂ £ 150. Прямая х₁ + х₂ = 150 проходит через точки (150, 0) и (0, 150).

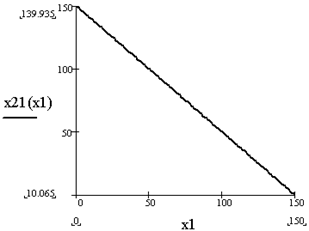
Рис. 2. Решением первого неравенства является нижняя полуплоскость

Второе ограничение по лавсану 2 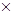х₁ + 0.5 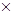х₂ £ 240. Прямая 2 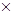х₁ + 0.5 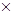х₂ = 240 проходит через точки (120, 0) и (0, 480). Третье ограничение по шерсти х₁ + 3.5 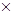х₂ £ 350. Добавим четвертое ограничение по количеству мужских костюмов х₂ ³ 60. Решением этого неравенства является полуплоскость, лежащая выше прямой х₂ = 60. На рис.3. заштрихована область допустимых решений.

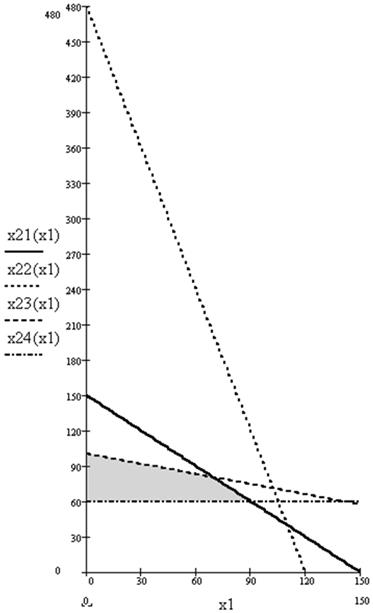
Рис. 3. Заштрихована область допустимых решений.

Для определения направления движения к оптимуму построим вектор-градиент Ñ, координаты которого являются частными производными целевой функции, т.е.

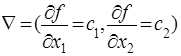= (10;20).

Что бы построить этот вектор, нужно соединить точку (10;20) с началом координат. При максимизации целевой функции необходимо двигаться в направлении вектора-градиента, а при минимизации – в противоположном направлении. Для удобства можно строить вектор, пропорциональный вектору Ñ. Так, на рис. 2.1.6. изображен вектор градиент (30;60).

В нашем случае движение линии уровня будем осуществлять до ее выхода из области допустимых решений. в крайней, угловой точке достигается максимум целевой функции. Для нахождения координат этой точки достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума:

х₁ + 3.5 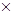х₂ = 350

х₁ + х₂ = 150

Отсюда легко записать решение исходной ЗЛП: max f(x) = 2300 и достигается при x1=70 и x2=80 (рис. 4.)

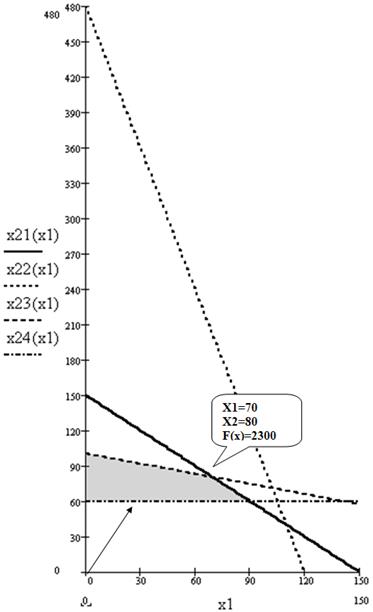
Рис.4. Максимум целевой функции достигается в точке (70, 80)

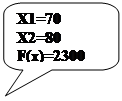Задача 2. Для изготовления двух видов продукции А₁ и А₂ используют три вида ресурсов S₁, S₂, S₃, запасы которых составляют 18, 15 и 5 усл. ед. Расход ресурсов на 1 ед. продукции приведен в таблице:

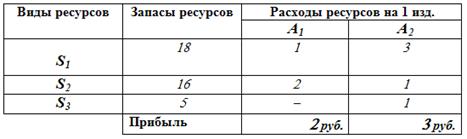
Необходимо составить такой план производства продукции, который обеспечит наибольшую прибыль от ее реализации.

Составим экономико-математическую модель (ЭММ) задачи.

Пусть надо выпустить изделий A₁ – x₁ шт., а изделий А₂ – x₂ шт. Тогда прибыль

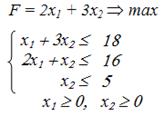
Date: 2015-07-25; view: 600; Нарушение авторских прав