Симплексный метод решения задачи линейного программирования

Для решения ЗЛП существует универсальный метод – метод последовательного улучшения плана или симплекс-метод, который состоит из двух вычислительных процедур: симплекс-метода с естественным базисом и симплекс-метода с искусственным базисом (М-метод).

Выбор конкретной вычислительной процедуры осуществляется после приведения исходной ЗЛП к каноническому виду (КЗЛП):

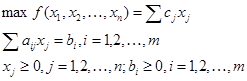
В теории линейного программирования (ЛП) показано, что оптимальное решение ЗЛП связано с угловыми (крайними) точками многогранника решений, которым отвечают опорные планы (неотрицательные базисные решения системы уравнений КЗЛП). Каждый из опорных планов определяется системой m линейно независимых векторов, содержащихся в данной системе из n векторов А₁, А₂,…, А_n. Верхняя граница количества опорных планов, содержащихся в данной задаче, определяется числом сочетаний С_nm.

Задача 3. Получить решение по модели задачи об оптимальном использовании ограниченных ресурсов (решить ЗЛП):

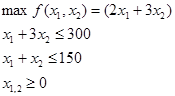
Приведем задачу к каноническому виду путем введения дополнительных переменных x 3 и x4:

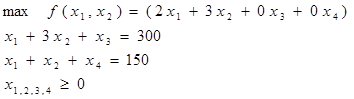
Найдем все опорные планы КЗЛП. Используя метод Жордана-Гаусса выписываем все базисные решения системы уравнений:

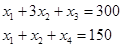
Последовательно будем иметь:

Х₁=(0,0,300,150); Х₂=(150,0,150,0); Х₃=(0,150,-150,0); Х₄=(75,75,0,0); Х₅=(300,0,0,-150); Х₆=(0,100,0,50).

Среди этих базисных решений четыре опорных:

Х₁=(0,0,300,150); Х₂=(150,0,150,0); Х₄=(75,75,0,0); Х₆=(0,100,0,50).

Указанным опорным планам на рис. 5 отвечают соответственно следующие угловые точки и значения ЦФ в них:

А(0,0) и f(0,0)=0; Д(150,0) и f(150,0)=300; С(75,75) и f(75,75)=375; В(0,100) и f(0,100)=300.

Согласно теории ЛП оптимальное решение содержится среди опорных планов.

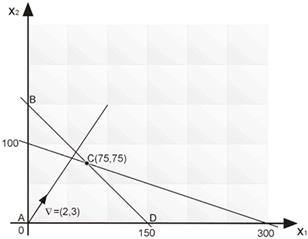
Рис.5

Таким образом, максимальное значение, равное 375, целевая функция f(x₁,x₂) достигает на опорном плане Х₄=(75,75,0,0), т.е. оптимальное решение рассматриваемой ЗЛП: x₁ = 75, x₂ = 75.

Понятно, что при больших m и n найти оптимальный план, перебирая указанным выше способом (прямым перебором) все опорные ЗЛП весьма трудно. Поэтому необходимо иметь схему, позволяющую осуществлять упорядоченный переход от одного опорного плана к другому. Такой схемой является симплексный метод.

Date: 2015-07-25; view: 489; Нарушение авторских прав