Численные методы решения обыкновенных дифференциальных уравнений. Метод Эйлера и методы Рунге-Кутта для решения дифференциальных уравнений

Суть метода Эйлера заключается в переходе от бесконечно малых приращений в уравнении к конечным: 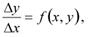(1)

т.е. в замене производной приближенным конечно-разностным отношением:

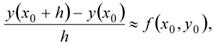
где h = ∆х - шаг интегрирования.

Отсюда 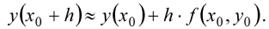(3)

Рассматривая приближенное решение в точке 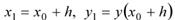как новые начальные условия, можно по формуле (3) найти значение искомой функции у(х) в следующей точке. В общем случае формула Эйлера имеет вид: 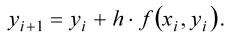(4)

Метод Эйлера может быть интерпретирован геометрически следующим образом: функцию у(х) заменяют ломаной, представляющей собой отрезки касательных к этой функции в узлах (рис. 5.1).

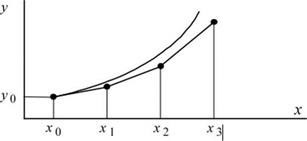
Рис. 5.1. Метод Эйлера

Достоинствами метода Эйлера являются его простота и наглядность, недостатками - относительно невысокая точность (он имеет первый порядок точности) и систематическое накопление ошибки. Точность и устойчивость решения в значительной степени зависят от величины шага интегрирования. Для оценки погрешности и выбора шага может быть применена формула Рунге .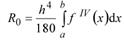

Методы Рунге-Кутта второго порядка

Методы Рунге-Кутта второго порядка основаны на разложении функции у(х) в ряд Тейлора и учете трех его первых членов (до второй производной включительно).

Метод Рунге-Кутта второго порядка с полным шагом реализуется по формуле:

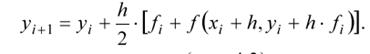(6.1.)

Его геометрическая интерпретация (рис. 6.1.) заключается в следующем:

1. Приближенно вычисляют значение функции в точке x_i+h по формуле Эйлера и наклон интегральной кривой в этой точке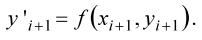

2. Находят средний наклон на шаге h: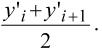

3. По этому наклону уточняют значение y_i+1 по формуле (6.1.).

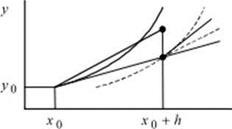Рис. 6.1. Метод Рунге-Кутта второго порядка с полным шагом

Формула метода Рунге-Кутта второго порядка с половинным шагом имеет вид

Рисунок 6.3. Метод Рунге-Кутта второго порядка с половинным шагом

Метод Рунге-Кутта четвертого порядка

Date: 2015-07-27; view: 10239; Нарушение авторских прав