Наслідки основної теореми алгебри

Наслідок 1. Многочлен n-го степеня має n коренів, де кожен корінь враховується стільки разів, скільки його кратність.

Доведення. Розглянемо деякий многочлен f(z)= a₀ zⁿ + a₁ z^n-1+ a₂ z^n-2 +...+a_n.

При n=0 многочлен має вигляд 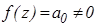і очевидно не має жодного кореня, тобто має 0 коренів.

Розглянемо випадок, коли n 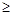1. Тоді за основною теоремою алгебри многочлен f(z) має прийнамні 1 корінь, тобто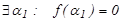

Застосуємо наслідок з теореми Безу:

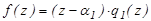
Якщо степінь 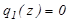, то теорему доведено. Якщо степінь , то застосуємо основну теорему алгебри:

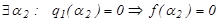
Продовжуючи таким чином, отримаємо

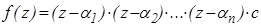
Отже, наслідок доведено.

Зауважимо, що .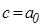

Мимохідь ми довели наслідок 2.

Наслідок 2. Будь-який многочлен можна розкласти на лінійні множники в області комплексних чисел.

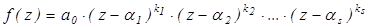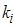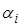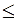, де - кратність кореня та s n.

Наслідок 3. Нехай задано два многочлена f(z) і g(z) степеня більшого або рівного n (n 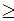1), значення яких збігається в n+1 точці, тобто

................................

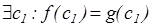
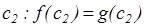
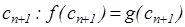
Тоді многочлени f(z) і g(z) є рівними (в формально-алгебраїчному сенсі).

Доведення. Припустимо супротивне. Нехай f(z) 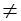g(z). Тоді утворимо многочлен h(z)=f(z)–g(z) (при цьому очевидо, що степінь h(z) 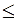n).

Тоді, згідно з 1 наслідком основної теореми алгебри, многочлен h(z) мусить мати не більше, ніж n коренів. Але існує n+1 точка, яка задовольняє умову: h(z)=0. Тому многочлен h(z) має n+1 корінь. Отримали суперечність, яка і доводить наслідок 3.

За допомогою цієї теореми можна довести еквівалентність двох підходів до поняття рівності многочленів.

Раніше ми довели, що якщо многочлени рівні в формально-алгебраїчному сенсі, то вони є рівними і в теоретико-функціональному.

Доведення оберненого. Степені многочленів є меншими або рівними деякого числа n, а многочлени збігаються в нескінченній множині точок. Виберемо серед них n+1 точку і застосуємо наслідок 3 основної теореми алгебри.

Date: 2015-07-27; view: 728; Нарушение авторских прав