
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Кинематический анализ рычажного механизма
|
|
2.2.1. Структурный анализ механизма
Степень подвижности механизма определим по формуле Чебышева:
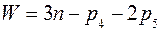 , (2.1)
, (2.1)
где 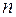 – число подвижных звеньев механизма;
– число подвижных звеньев механизма;
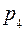 – число кинематических пар 4 класса;
– число кинематических пар 4 класса;
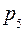 – число кинематических пар 5 класса; получим
– число кинематических пар 5 класса; получим
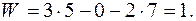
За начальное звено принимаем кривошип ОА, так как для него задан закон движения. Формула строения механизма в этом случае:
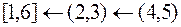 , (2.2)
, (2.2)
где [1,6] – начальный механизм I класса;
(2,3) – структурная группа II класса 2 вида;
(4,5) – структурная группа II класса 3 вида.
Таким образом, данный механизм является механизмом второго класса.
2.2.2. Построение заданного положения механизма
Примем масштаб изображения механизма на чертеже 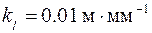 . Отрезки на чертеже будем обозначать со знаком “ ~ “.
. Отрезки на чертеже будем обозначать со знаком “ ~ “.
Длины звеньев на чертеже:
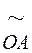 =35 мм;
=35 мм; 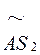 =30 мм;
=30 мм; 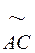 =45 мм;
=45 мм;
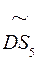 =60 мм;
=60 мм; 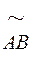 =105 мм;
=105 мм; 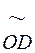 =100 мм.
=100 мм.
Текущее значение размера CD, соответствующее заданной угловой координате кривошипа 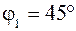 , определено построением:
, определено построением:
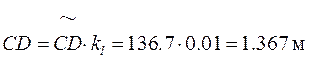 .
.
2.2.3. Построение плана скоростей
Кинематический анализ механизма выполняем для заданного положения механизма в порядке присоединения структурных групп согласно формуле (2.2).
Начальный механизм [1,6]
Скорость точки А
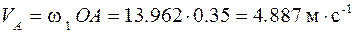 . (2.3)
. (2.3)
Примем масштабный коэффициент плана скоростей 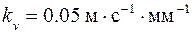 .
.
Вектор 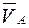 направлен из полюса плана скоростей pv перпендикулярно кривошипу ОА в сторону его вращения; конец этого вектора на плане скоростей – точка а. Длина вектора
направлен из полюса плана скоростей pv перпендикулярно кривошипу ОА в сторону его вращения; конец этого вектора на плане скоростей – точка а. Длина вектора 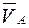 на плане
на плане
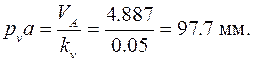 (2.4)
(2.4)
Группа (2,3 )
Скорость точки В:
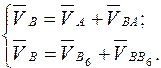 (2.5)
(2.5)
В первом уравнении вектор 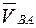 направлен перпендикулярно АВ. Точка В 6 неподвижна (
направлен перпендикулярно АВ. Точка В 6 неподвижна (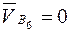 ) и конец вектора
) и конец вектора 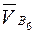 (точка b 6) совпадает с полюсом плана скоростей. Вектор
(точка b 6) совпадает с полюсом плана скоростей. Вектор 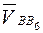 направлен параллельно направляющей.
направлен параллельно направляющей.
В результате построения находим точку b – конец вектора 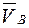 :
:
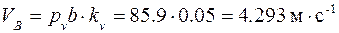 ;
; 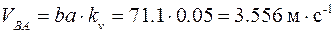 .
.
В этих формулах 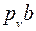 и
и 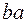 – длины (в миллиметрах) отрезков плана скоростей.
– длины (в миллиметрах) отрезков плана скоростей.
Угловая скорость звена механизма определяется по параметрам относительной скорости любых двух точек, принадлежащих этому звену.
Угловая скорость звена 2:
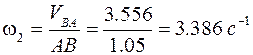 .
.
Скорости точек С и S 2 могут быть определены методом подобия, согласно которому точки, принадлежащие одному звену, образуют на плане механизма и на плане скоростей подобные фигуры, в данном случае – отрезки. Таким образом, из подобия отрезков имеем:
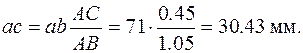 (2.6)
(2.6)
 (2.7)
(2.7)
Из плана скоростей найдем
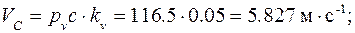
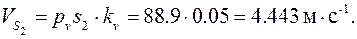
группа (4,5)
Скорость точки С 5:
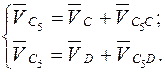 (2.8)
(2.8)
В первом уравнении вектор  направлен параллельно СD. Точка D неподвижна (
направлен параллельно СD. Точка D неподвижна (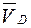 =0) и конец вектора
=0) и конец вектора 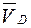 (точка d) совпадает с полюсом плана скоростей. Вектор
(точка d) совпадает с полюсом плана скоростей. Вектор 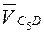 направлен перпендикулярно СD.
направлен перпендикулярно СD.
Из плана получим:
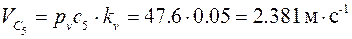 ;
;
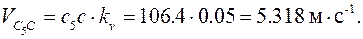
Угловая скорость звеньев 4 и 5:
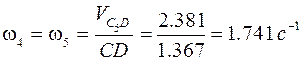 .
.
Скорость точки S 5 определим методом подобия:
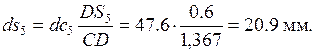 (2.9)
(2.9)
Скорость точки S 5:

2.2.4. Построение плана ускорений
Начальный механизм [1,6]
Ускорение точки А
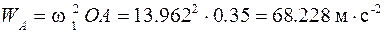 .
.
Примем масштабный коэффициент плана ускорений
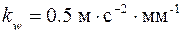 .
.
Вектор 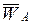 направлен параллельно звену ОА от точки А к точке О, откладываем этот вектор из полюса плана ускорений
направлен параллельно звену ОА от точки А к точке О, откладываем этот вектор из полюса плана ускорений 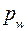 ; отрезок на плане ускорений
; отрезок на плане ускорений
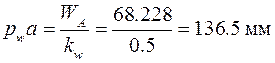 ;
;
конец вектора 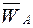 - точка а.
- точка а.
Группа (2,3)
Ускорение точки В
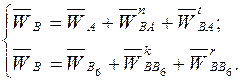 . (2.10)
. (2.10)
Вектор тангенциального ускорения 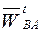 и вектор относительного ускорения
и вектор относительного ускорения 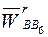 направлены параллельно векторам скоростей с одноименными нижними индексами; их длины определяются построением; остальные векторы правой части уравнений (2.10) также известны по направлению и могут быть найдены по величине.
направлены параллельно векторам скоростей с одноименными нижними индексами; их длины определяются построением; остальные векторы правой части уравнений (2.10) также известны по направлению и могут быть найдены по величине.
Так как точка В 6 принадлежит неподвижной направляющей, то её ускорение 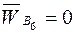 , угловая скорость
, угловая скорость  также равна нулю, и ускорение Кориолиса
также равна нулю, и ускорение Кориолиса
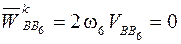 .
.
Вектор нормального ускорения 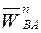 направлен параллельно звену АВ от точки B к точке A и имеет начало в точке a плана ускорений; его величина
направлен параллельно звену АВ от точки B к точке A и имеет начало в точке a плана ускорений; его величина
 ;
;
отрезок 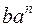 на плане ускорений
на плане ускорений
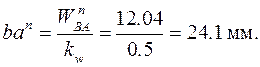
Совмещая начало вектора 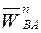 с точкой а на плане ускорений, а начало вектора
с точкой а на плане ускорений, а начало вектора 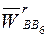 с полюсом плана ускорений и проведя линии действия векторов
с полюсом плана ускорений и проведя линии действия векторов 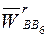 и
и 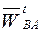 , получим в месте их пересечения точку b. Ускорение
, получим в месте их пересечения точку b. Ускорение  найдем, соединив точку b с полюсом плана ускорений; его величина
найдем, соединив точку b с полюсом плана ускорений; его величина
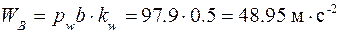 ;
;
тангенциальное ускорение
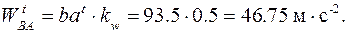
Угловое ускорение звена механизма определяется по параметрам тангенциальной составляющей относительного ускорения двух любых точек, принадлежащих этому звену.
Угловое ускорение звена 2:
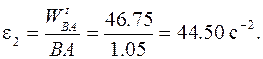
Ускорения точек S 2 и С определим методом подобия; из соотношений (2.6) и (2.7) получим
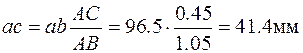 ;
;
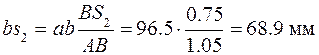 .
.
Из плана найдем ускорения
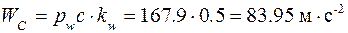 ,
,
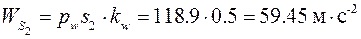 .
.
группа (4,5)
Ускорение точки С 5:
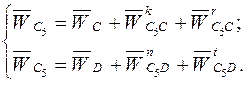 (2.11)
(2.11)
Вектор тангенциального ускорения 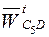 и вектор относительного ускорения
и вектор относительного ускорения 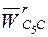 направлены параллельно векторам скоростей с одноименными нижними индексами; их длины определяются построением; остальные векторы правой части уравнений (2.11) также известны по направлению и могут быть найдены по величине.
направлены параллельно векторам скоростей с одноименными нижними индексами; их длины определяются построением; остальные векторы правой части уравнений (2.11) также известны по направлению и могут быть найдены по величине.
Ускорение Кориолиса
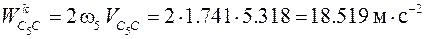 ;
;
отрезок на плане ускорений
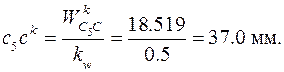
Направление ускорения 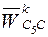 совпадает с направлением вектора
совпадает с направлением вектора 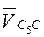 после его поворота в сторону вращения звена 5 на 90°.
после его поворота в сторону вращения звена 5 на 90°.
Нормальное ускорение
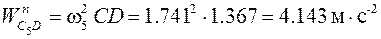 ;
;
величина отрезка 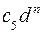 на плане ускорений
на плане ускорений
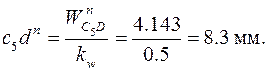
Вектор 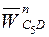 направлен параллельно CD от точки C к точке D; его начало помещают в точке d, то есть в полюсе плана ускорений. Согласно уравнениям (2.11) в конце вектора
направлен параллельно CD от точки C к точке D; его начало помещают в точке d, то есть в полюсе плана ускорений. Согласно уравнениям (2.11) в конце вектора 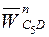 проведем линию действия ускорения
проведем линию действия ускорения 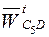 . Начало вектора
. Начало вектора 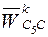 поместим в точке с плана ускорений, а к его концу пристроим линию относительного ускорения
поместим в точке с плана ускорений, а к его концу пристроим линию относительного ускорения 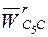 . В месте пересечения линий последних векторов уравнений (2.11) получим точку с5 – конец вектора
. В месте пересечения линий последних векторов уравнений (2.11) получим точку с5 – конец вектора 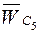 .
.
Из построения получим:
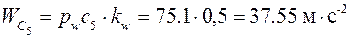 ;
;
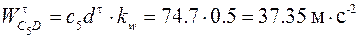 .
.
Угловое ускорение звеньев 4 и 5:
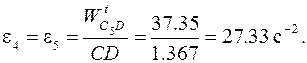
Положение точки 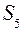 на плане определяется методом подобия из соотношения (2.9):
на плане определяется методом подобия из соотношения (2.9):
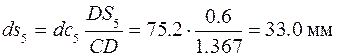 .
.
Ускорение точки 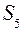 :
:
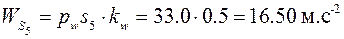 .
.
Date: 2015-07-27; view: 392; Нарушение авторских прав