Силовой расчет редуктора

Исходными данными для силового расчета являются результаты кинематического расчета редуктора и величина момента полезного сопротивления 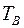на выходном валу редуктора, равная среднему значению движущего момента 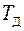на валу кривошипа рычажного механизма

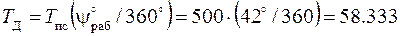Н∙м,

где 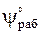- угол качания кулисы, нагруженной моментом (из задания на рычажный механизм).

Приняты следующие КПД кинематических пар: вращательной - 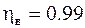, зацепления - .

Целью расчета является определение энергетических и силовых соотношений редуктора.

1.3.1 Расчет с учетом потерь мощности на трение

Расчет с учетом потерь мощности на трение выполняем с помощью уравнений баланса мощностей и равновесия. Коэффициент полезного действия в уравнениях баланса мощностей является сомножителем при подводимой мощности, то есть при положительном слагаемом уравнения.

1)Уравнение энергетического баланса для выходного вала

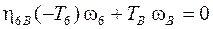. (1.3)

Так как мощность 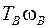, снимаемая с выходного вала, отрицательна и угловая скорость 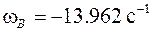, то момент 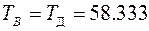Н∙м является положительным. Очевидно, что уравнение (1.3) справедливо только при .

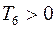2) Уравнение баланса мощностей для рядовой кинематической цепи

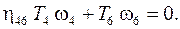(1.4)

Так как в этом уравнении угловые скорости 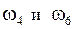имеют противоположные знаки, то моменты 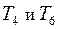будут одного знака, т.е. .

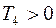3) Уравнение баланса мощностей для промежуточного вала

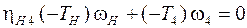. (1.5)

Так как второе слагаемое – отрицательно, то первое – положительно, отсюда .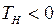

4) Для планетарной ступени:

уравнение баланса мощностей в обращенном движении

;

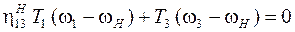уравнение равновесия

.

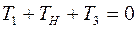Так как в уравнении баланса мощностей знаки относительных скоростей разные, т.е. 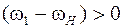и 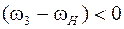, то знаки моментов 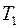и должны быть одинаковыми. Из уравнения равновесия следует, что при отрицательном моменте 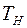моменты 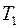и – положительны. Тогда мощность 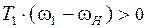, и колесо 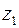в обращенном механизме является ведущим.

Уравнения, записанные для планетарной ступени, образуют систему, решение которой имеет вид

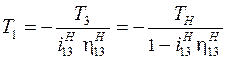. (1.6)

5) Уравнение баланса мощностей для входного вала

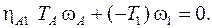(1.7)

Т.к. 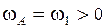, то второе слагаемое отрицательно, а первое – положительно, при этом 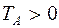, что подтверждает правильность определения знаков моментов.

6) Уравнение баланса мощностей для механизма

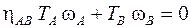, (1.8)

где 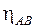– коэффициент полезного действия редуктора.

Определим по приведенным уравнениям моменты на звеньях механизма при заданном моменте 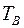и коэффициентах полезного действия

;

.

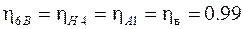Из уравнения (1.3) получим момент на колесе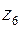

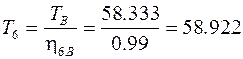Н∙м.

Из уравнения (1.4) найдем момент на колесе :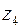

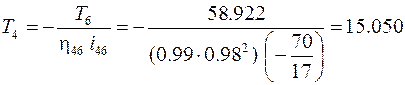Н∙м.

Из уравнения (1.5) момент на водиле

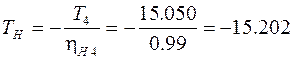Н∙м.

Из уравнения (1.6) для планетарной ступени получим:

момент на колесе :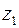

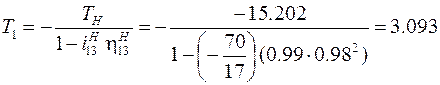Н∙м;

момент на колесе :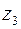

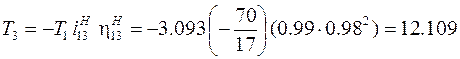Н∙м.

Из уравнения (1.7) найдем величину подводимого момента:

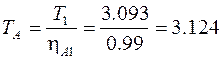Н∙м.

Из уравнения (1.8) найдем коэффициент полезного действия редуктора:

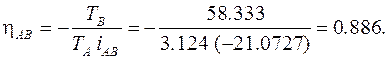
1.3.2. Расчет без учета потерь мощности на трение

1) Определение моментов на звеньях механизма

Для расчета величин моментов воспользуемся формулами (1.3)…(1.7). Полагая 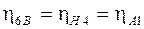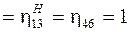, получим:

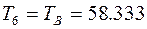Н∙м;

Н×м;

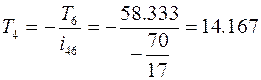Н∙м;

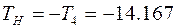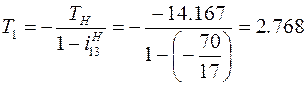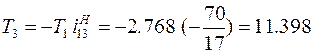Н∙м;

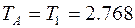Н∙м;

Н∙м.

Из формулы (1.8) определим КПД

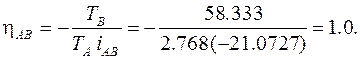
Величина 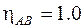подтверждает правильность расчета моментов.

В данном механизме замкнутая мощность отсутствует.

Мощности на звеньях:

кВт;

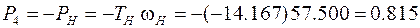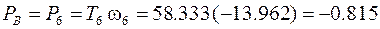кВт;

кВт.

1) Силовой расчет методом окружных сил

В рассматриваемом примере числа зубьев колес 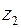и 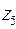по условию соосности были получены дробными, а затем округлены до целых, поэтому для планетарной ступени межосевое расстояние 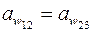следует вычислять по формулам

,

.

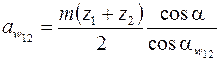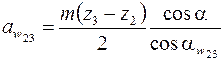Примем 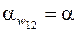, получи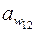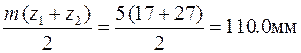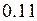м

= = м,

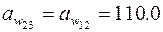мм = 0.11м;

для рядовой ступени

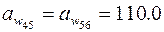мм = 0.11м.

Диаметры начальных окружностей для планетарной ступени

мм = 0.085м;

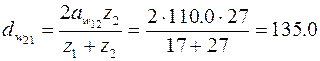мм = 0.135м;

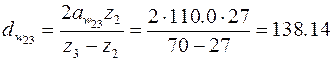мм = 0.138м;

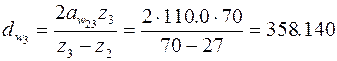мм = 0.358м.

Диаметры начальных окружностей для рядовой ступени

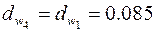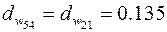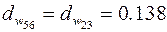м; м; 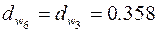м;

м.

Силовой расчет методом окружных сил проводим согласно схеме, изображенной на рис. 1.2.

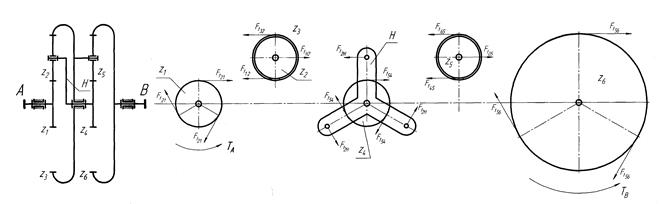
Рис. 1.2.

Для расчета величин окружных сил 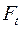в зацеплениях колес используем условия равновесия моментов всех внешних сил, действующих на каждое из звеньев механизма.

Момент 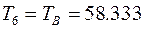Н·м;

из уравнения моментов для колеса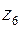

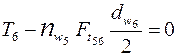
окружное усилие:

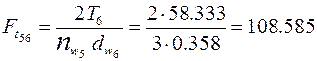Н.

Для связанного колеса 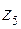из уравнения моментов:

,

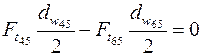получим

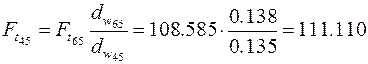Н.

Из уравнения моментов для узла водила Н с колесом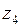

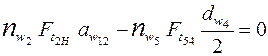
получим:

Н.

Для сателлита 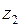из уравнения моментов:

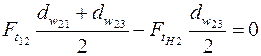
получим

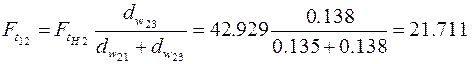Н;

тогда

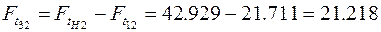Н.

Из уравнения моментов для колеса 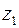получим момент на входном валу

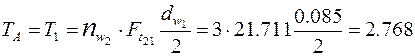Н·м,

что совпадает с величиной этого момента, рассчитанного выше с помощью уравнений баланса мощностей.

Распечатка результатов расчета зубчатого механизма

по программе FORCE

Силовой анализ зубчатого редуктора по схеме 10

методом окружных сил

ИСХОДНЫЕ ДАННЫЕ

Модуль, мм: m = 5.000.

Числа зубьев колес планетарной ступени: z1 = 17;

z2 = 27;

z3 = 70.

Число сателлитов в планетарной ступени: nW2 = 3.

Числа зубьев колес рядовой цепи: z4 = 17;

z5 = 27;

z6 = 70.

Число связанных колес z5 в рядовой цепи: nW5 = 3.

Момент сопротивления на выходном валу, Н∙м: TB = 58.333.

РЕЗУЛЬТАТЫ РАСЧЕТОВ

Передаточное отношение редуктора: iAB = -21.073.

Радиус водила планетарной ступени, мм: rH = 110.000.

Диаметры начальных окружностей колес, мм: dw1 = 85.000;

dw21 = 135.000;

dw23 = 135.000;

dw3 = 358.140.

Межосевое расст. в ряд. цепи z4z5z6, мм:aw45 = 110.000.

Диаметры начальных окружностей колес, мм: dw4 = 85.000;

dw54 = 135.000;

dw56 = 138.140;

dw6 = 358.140.

Окружные силы в кинематических парах, Н:Ft56 = 108.585;

Ft45 = 111.110;

Ft0 = 219.696;

FtH = 42.929;

Ft32 = 21.218;

Ft12 = 21.711.

Движущий момент на входном валу, Н∙м: TA = 2.768.

Date: 2015-07-27; view: 865; Нарушение авторских прав