П°3.2 Примеры решения задач на построение методом движения

Задача №1 (метод параллельного переноса)

Построить трапецию по двум ее диагоналям d₁ и d₂, средней линии m и одному из углов φ.

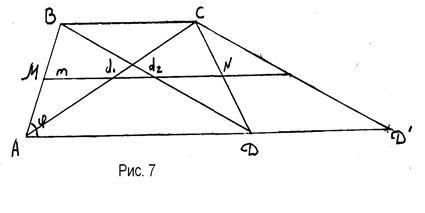
1) АНАЛИЗ (Рис. 7)

Предположим, что задача решена, т. е. АВСD – искомая трапеция, |АС| = d₁, |BD| = d₂, 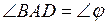, |MN| = m – средняя линия трапеции АВСD. |BС| < |AD|.

Рассмотрим параллельный перенос 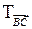: 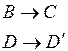, следовательно 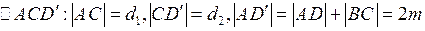т. е. треугольник АСD' можно построить.

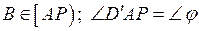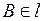, , причем l: 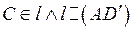, значит .

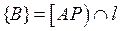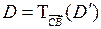
2) 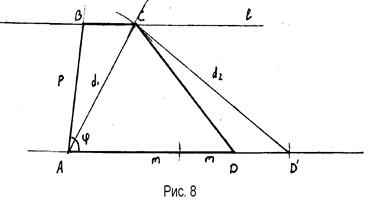ПОСТРОЕНИЕ (Рис. 8)

Строим:

1. 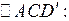|АС| = d₁, |СD'| = d₂, |АD'| = 2m

2. :

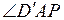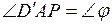
3. l: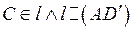

4.

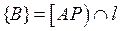
5. D: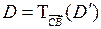

АВСD – искомая трапеция.

3) ДОКАЗАТЕЛЬСТВО

По построению |АС| = d₁, |СD'| = |ВD| = d₂ - по свойствам параллельного переноса, 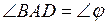- по построению. Аналогично 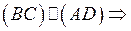[BC], [AD] – основания трапеции, |АD| + |ВС| = 2 m, т. е. 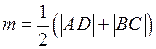, т. е. m – средняя линия, следовательно, АВСD – искомая трапеция.

4) ИССЛЕДОВАНИЕ

Задача имеет единственное решение, с точностью до движения, в том случае, когда d₂ - d₁ < 2 m < d₂ + d₁. В случае, если это неравенство не выполняется, задача решений не имеет.

Задача №2 (метод поворота)

В данный квадрат вписать равносторонний треугольник, одна из вершин которого дана (на стороне квадрата).

1) АНАЛИЗ

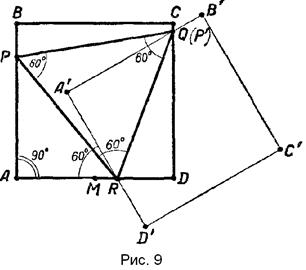
Предполагаем задачу решенной; в данный квадрат ABCD вписан равносторонний треугольник PQR (Рис. 9), причем вершина R — данная точка.

Так как каждый угол равностороннего треугольника содержит 60°, то при повороте 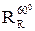: квадрат ABCD → A'B'C'D', R → R, P → Q(P'), причем: 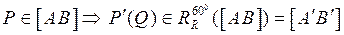, но 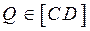, т. е. 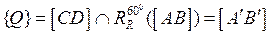. Точку Q можно построить. Точка 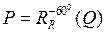, т. е. точку P тоже можно построить.

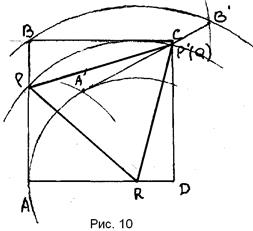
2) ПОСТРОЕНИЕ (Рис. 10)

Строим:

1. [А'В']: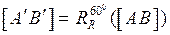

2. Q: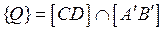

3. P: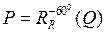

Треугольник PQR – искомый.

3) ДОКАЗАТЕЛЬСТВО

Доказательство следует из анализа и того, что поворот является движением плоскости, а, значит, сохраняет расстояние между любыми двумя точками.

4) ИССЛЕДОВАНИЕ.

Так как при повороте вокруг точки R на 60⁰ всегда точка А → А', расположенную внутри квадрата, точка В → В', расположенную вне квадрата, то пересечение [А'В'] со стороной квадрата ABCD всегда имеет место. Следовательно, задача всегда имеет решение и притом единственное.

Задача №3. (Метод осевой симметрии)

Даны прямая l и две точки А и В, лежащие по одну сторону от данной прямой. Требуется на прямой l найти такую точку Х, чтобы ломаная АХВ имела наименьшую длину.

1) АНАЛИЗ

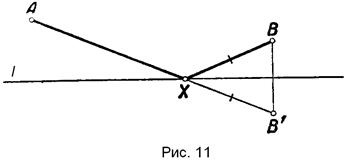Пусть задача решена и точка Х – искомая. Рассмотрим симметрию относительно оси l, тогда В' = S _l (B). При любом положении Х на прямой будем иметь: ХВ = ХВ', длина ломаной АХВ равна длине ломаной АХВ'. Поэтому точка В может быть заменена точкой В', и достаточно найти такое положение точки Х, при котором ломаная АХВ' имеет минимум. Очевидно, что это будет иметь место, когда ломаная АХВ' является прямой (рис. 11). Получили возможное построение.

2) ПОСТРОЕНИЕ

Строим

1. В': В' = S _l (B)

2. (АВ')

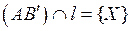- искомая

3) ДОКАЗАТЕЛЬСТВО

Доказательство следует из анализа построения

4) ИССЛЕДОВАНИЕ

Решение всегда существует, причем единственное, поскольку точки А и В' лежат по разные стороны от прямой l.

Date: 2015-07-27; view: 3430; Нарушение авторских прав