Метод пересечения решения задачи на построение

п°2.1 Сущность метода пересечения (метод ГМТ).

Метод пересечения множеств применяется в задачах, решение которых сводится к построению одной точки, удовлетворяющей двум условиям a₁ и a₁. При этом определяют два множества точек плоскости M₁ и М₂, всевоз­можных точек плоскости π, удовлетворяющих условиям a₁ и a₁ соответст­венно. Искомая точка принадлежит пересечению М₁ и М₂. Ясно, что в зада­чах на построение рассматриваются только те множества, которые состоят из прямых и окружностей. Они называется конструктивными.

Простейшие построения при методе пересечения - геометрические места точек на плоскости.

Определение. Геометрическим местом точек (ГМТ) плоскости, обла­дающих свойством а, называется множество всех, точек плоскости, для ко­торых выполняется условие а.

При решении задачи на построение методом пересечения будем исполь­зовать следующие ГМТ плоскости:

1°. Множество точек плоскости, удаленных от данной точки О на данное расстояние r, - окружность 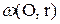с центром О и радиусом r.

2 °. Множество всех точек плоскости, удаленных на данное расстояние d от данной прямой l - объединение двух прямых l₁ и l₂, параллельных l и удаленных от l на расстояние d.

3°. Множество всех точек плоскости, каждая из которых равноудалена от двух данных различных точек А и В, - серединный перпендикуляр p к от­резку [АВ].

4°. Множество всех точек плоскости, каждая из которых равноудалена от двух данных параллельных прямых l₁ и l₂, - прямая l, параллельная l₁ и l₂ и являющаяся для них осью симметрии.

5°. Множество всех точек плоскости, каждая из которых равноудалена от двух пересекающихся прямых l₁ и l₂ - объединение двух перпендикулярных прямых p₁ и р₂, содержащих биссектрисы углов, образованных прямыми l₁ и l₂ при пересечении.

6°. Множество всех точек плоскости, из которых данный отрезок [АВ]виден под прямым углом - множество 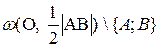, где О - сере­дина [АВ|.

7°. Множество всех точек плоскости, из которых данный отрезок виден под данным углом φ, где 0°<φ<180°, φ≠90°, есть объединение двух откры­тых дуг окружности с концами А и В, симметричных, относительно (АВ).

8°. Множество всех точек плоскости, для каждой из которых отношение расстояний до двух данных различных точек А и В постоянно и отлично от единицы, есть окружность с центром на прямой АВ - окружность Аполло­ния.

Построения 1° - 8° будем считать простейшими и при решении задач на построение не будем описывать построения этих фигур.

Далее более обстоятельно рассматриваются построения 7° и 8°.

7°. Построить множество всех точек плоскости, из которых данный отрезок [AB] виден под данным углом φ, где 0°<φ<180°, φ≠90°.

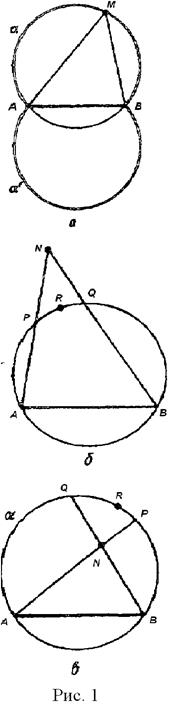
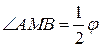
Решение. Пусть точка М принадлежит иско­мому множеству. Опишем окружность α вокруг треугольника АМВ (рис. 1 а). Обозначим меру дуги этой окружности, не содержащей точки М, через . . 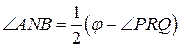Ясно, что из всех точек дуги АМВ отрезок АВ виден под данным углом. Пусть точка N принадлежит той же полуплоскости с границей АВ, что и точка М, но лежит вне окружности α (рис. 1 б). Тогда 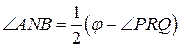, т. е. из точки N отрезок АВ виден под углом, меньшим данного. Пусть точка N лежит в той же полуплоскости относительно прямой АВ, что и точка М, но находится внутри окружности α (рис. 1 в). Тогда 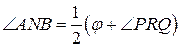. Таким образом, точка рассматриваемой полуплоскости тогда и только тогда принадлежит искомому множеству, когда она является точкой дуги АМВ. Осуществив аналогичные рассуждения для точек другой полуплоскости, получим: иско­мое множество точек представляет собой две от­крытые дуги, симметричные относительно (АВ). Если данный угол равен прямому, то каждая из дуг является полуокружностью, а все множество - окружностью без точек А и В. Итак, дан отрезок [АВ] и 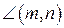такой, что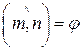

1) 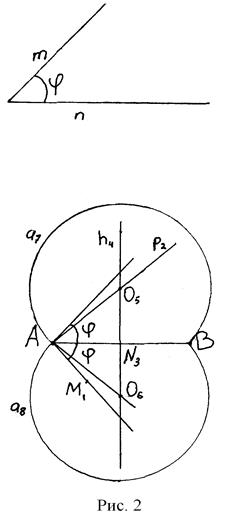Отложим от луча АВ данный угол .

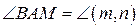Строим:

2) прямую р₂, перпендикулярную (AM₁) и проходящую че­рез точку А (рис. 2);

3) точку N₃ — середину отрезка АВ;

4) серединный перпендикуляр h₄ отрезка АВ.

5) Определим точку O₅ пересечения прямой р₂ и перпендикуляра h₄.

Далее строим:

6) точку О₆, симметричную точке O₅ относительно прямой АВ;

7) окружность (а₇: );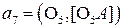

8) окружность (а₈: .

Открытые с концами А и В дуги окружностей а₇ и а₈ искомые.

Нетрудно показать, что разобранный метод построения приводит к искомому множеству. Действительно, 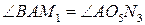(как углы со взаимно перпендикулярными сторонами). Так как угол 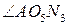равен половине центрального угла 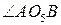, то 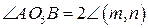. Отсюда дуга ок­ружности О₇, определяемая центральным углом , равна удвоенно­му данному углу, а вписанные углы, опирающиеся на нее, равны . Утверждение доказано.

8°. Окружность Аполлония.

Рассмотрим задачу: «Найти множество всех точек плоскости, для которых отношение расстояний до двух данных точек равно положительному числу λ, отличному от единицы».

Решение. Пусть А и В — данные точки. На прямой АВ существуют точки М и N, для которых |AM|:|МB|=|AN|:|NB|=λ Обозначим через X точку искомого множества (рис. 3 а). Тогда |АХ|:|ХВ|=|АМ|:|МВ|=λ. В треугольнике АХВ точка М делит основание АВ на отрезки, которые относятся так же, как длин боковых сторон АХ и ХВ. Поэтому из теоремы о биссектрисе внутреннего угла треугольника следует, что [ХМ] — биссектриса треугольника АХВ.

Аналогично показывается, что XN — биссектриса внешнего угла ВХР треугольника АХВ. Так как углы АХВ и ВХР смежные, то их биссектрисы взаимно ортогональны. Из точки X отрезок [MN] виден под прямым углом, следовательно, точка X лежит на окружности, построенной на [MN] как на диаметре.

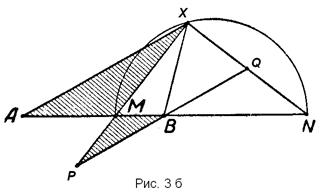Обратно, возьмем произвольную точку окружности, диаметр которой равен |MN| (рис. 3 б). 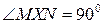. Пусть точка В лежит между М и N. Про­ведем через нее прямую, параллельную (АХ), Р и Q—точки ее пересечения с (MX) и (NX). Тогда треугольники АХМ и РМВ подобны друг другу. От­сюда:

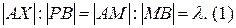
Треугольники BQN и AXN также подобны между собой. Получим:

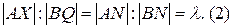
Из формул (1) и (2) следует, что |BQ|=|PB|. Поэтому отрезок ВХ являет­ся медианой прямоугольного треугольника PXQ. Так как медиана прямо­угольного треугольника равна половине гипотенузы, т. е. |ВХ| = |РВ|, то из (1) следует равенство | АХ |: | ВХ | = X. Утверждение доказано.

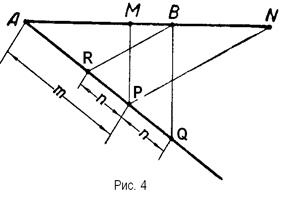
Для построения окружности Аполлония необходимо определить точки М и N прямой АВ, удовлетворяющие условию: |AM|:|МB|=|AN|:|NB|=λ. В дальнейшем будем предполагать, что число X задано в виде отношения длин двух отрезков: λ = m: n. Способ построения точек М и N показан на рисунке 4. Отрезки PR и PQ равны n, отрезок АР равен m. Прямая MP параллельна прямой BQ, (BR) параллельна (PN). Из теоремы Фалеса следует: [AM]:[МB] = m: n, [AN]:[NB] = m: n,

Мы предположили, что λ ≠ 1. Если λ = 1, то искомое множество является серединным перпендикуляром отрезка [АВ].

Date: 2015-07-27; view: 4248; Нарушение авторских прав