Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Ядерные реакции. · Запись ядерной реакции

⇐ ПредыдущаяСтр 45 из 45

· Запись ядерной реакции

,

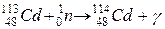
где X и Y – исходное и конечное ядра; а и b – бомбардирующая и испускаемая в ядерной реакции частицы; 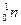- нейтрон; γ – фотон.

· Энергия ядерной реакции

,

где m 1 и m 2 – массы покоя ядра-мишени и бомбардирующей частицы; (m 3 + m 4) – сумма масс покоя ядер продуктов реакции.

 

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. Найти энергию связи ядра урана и энергию связи, приходящуюся на нуклон. Масса ядра урана m я = 237,99768 а.е.м.

Решение: Энергию связи находим по формуле:

E св= [ Z · m р + (A – Z) m n – m я] c 2,

где m p = 1, 00783 а.е.м. – масса протона; m n = 1, 00867 а.е.м. – масса нейтрона; А – массовое число; Z – порядковый номер элемента; с – скорость света в вакууме.

Подставляя данные, получим

E св= [92·1,00783 + (238 – 92)1,00867 – 237,99768]931 = 1851 МэВ

По определению удельная энергия связи:

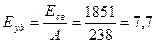МэВ/нуклон.

 

Пример 2. Радиоактивный натрий 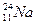распадается, выбрасывая 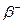-частица. Период полураспада натрия Т1/2 = 14,8ч. Вычислить количество атомов 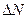, распавшихся в m =1 мг данного радиоактивного препарата за t =10 ч.

Решение: Число распавшихся атомов за время t: ,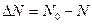

где N 0– число нераспавшихся атомов в начальный момент времени в 1 мг , N – число нераспавшихся атомов по прошествии времени t.

Используя закон радиоактивного распада 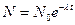, запишем для нашего случая: .

Учитывая, что , получим

Поскольку в одном моле содержится число атомов, равное постоянной Авогадро, то в данной массе содержится число атомов N0, равное произведению числа молей 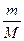на постоянную Авогадро NА: , молярная масса натрия М = 24·10-3 кг.

Общее выражение получим: .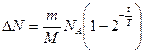

Подставив данные, получим:

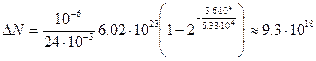атомов.

Пример 3. Вычислить толщину слоя половинного ослабления х ½ параллельного пучка γ- излучения для воды, если линейный коэффициент ослабления μ = 0,047 см-1.

Решение: При прохождении γ- излучения через слой вещества происходит его поглощение за счет трех факторов: фотоэффекта, эффекта Комптона и образование электронно-позитронных пар. В результате действия этих трех факторов интенсивность γ-излучения экспоненциально убывает в зависимости от толщины слоя.

Пройдя поглощающий слой толщиной, равной толщине слоя половинного ослабления , пучок γ-излучения будет иметь интенсивность .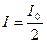

Подставив значения I и x 1/2 в формулу, получим ,

после сокращения на I 0 , получаем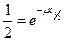

Прологарифмировав выражение, получим искомое значение толщины слоя половинного ослабления: 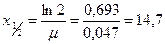см.

Пример 4. При захвате ядром лития 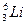медленного нейтрона 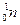образуется изотоп водорода – тритий . Реакция экзотермическая с выделением энергии ∆ Е = 5,6 МэВ. Какая еще частица образуется в результате этой реакции? Какая энергия Е1 приходится на ядро трития, а какая Е 2 – на эту частицу? Кинетическими энергиями ядра лития и нейтрона до реакции можно пренебречь.

Решение: Ядерная реакция пройдет по схеме: .

Поскольку кинетическими энергиями до реакции пренебрегаем, то их суммарный импульс равен 0, значит, суммарный импульс частиц – продуктов реакции – тоже равен 0: , (1)

где υ1 – скорость трития, υ2 – скорость альфа-частицы.

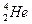Энергия ∆Е, выделившаяся в результате реакции, равна сумме кинетических энергий Е1 и Е2 трития и альфа-частицы , образовавшихся в результате реакции: 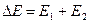, (2)

где и ,

поэтому . (3)

Из уравнения (1) можно найти скорость альфа-частицы

. (4)

Подставим (4) в (3):

.

Отсюда . Из (2) найдем Е2: .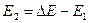

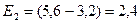Произведем вычисления: МэВ, МэВ.

 

Пример 5. Найти энергию, выделяющуюся при реакции .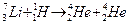

Решение: Изменение энергии при ядерной реакции определяется как:

.

Сумма масс исходных частиц

а.е.м.

Сумма масс образовавшихся частиц

а.е.м.

Таким образом, дефект масс 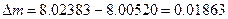а.е.м.

Тогда энергия, выделяющаяся при данной реакции

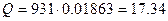МэВ.

 

КОНТРОЛЬНАЯ РАБОТА № 1

 

1. Точка движется в плоскости 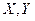причем 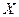меняется по закону х = 50 t (см), а y по закону y = 200 t – 25 t 2. Найти угол между скоростью и полным ускорением в конце 3 секунды. Ответ дать в градусах.

2. Материальная точка движется в плоскости XOY, и при этом её координаты изменяются с течением времени по закону x = 2 sin ωt и y = 2 cos ωt, где ω – константа. Какова траектория точки?

3. Движение материальной точки по прямолинейной траектории описывается уравнением 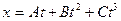, где А = 1 м/с, В = -2 м/с2 и С = 4 м/с3. Найти в момент t 1 = 3 с координату точки, ее скорость и ускорение.


4. Кинематические уравнения движения двух материальных точек имеют вид 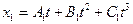и 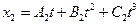, где В 1 = 4 м/с2, С 1 = -3 м/с3, В 2 = -2 м/с2, С 2 = 1 м/с3. Определите момент времени, для которого ускорения этих точек будут равны ().

5. Для материальной точки, движущейся по оси ОХ, зависимость координаты от времени выражается уравнением x = 6 – 4 t + t 2, в котором все величины заданы в единицах СИ. Определить через t 1 = 5 с после начала движения координату точки, её скорость и пройденный путь.

6. Материальная точка движется по окружности радиуса R так, что зависимость угла поворота от времени задана уравнением 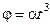. Найти полное ускорение точки как функцию времени.

7. Материальная точка движется по окружности радиуса 4 м. Зависимость пути от времени задана уравнением 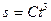, где С = 0,02 м/с3. Найти ускорение и его тангенциальную и нормальную составляющие в момент, когда скорость точки равна υ1 = 6 м/с.

8. Определить минимальную скорость движения пожарного автомобиля массой 20 тонн по выпуклому мосту, имеющему вид дуги окружности радиусом 75 метров и рассчитанному на максимальную покоящуюся нагрузку массой 14 тонн.

9. При одномерном движении с постоянным ускорением зависимости координаты и скорости частицы от времени описываются соотношениями: 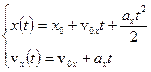. Установить связь между координатой частицы и ее скоростью.

10. Материальная точка совершает два последовательных перемещения. Вектор первого перемещения направлен под углом α1 = 300 к оси ОХ, причем на этом участке точка движется прямолинейно и равномерно со скоростью υ1 = 10 м/с. Вектор второго перемещения направлен под углом α2 = 900 к оси ОХ и его модуль вдвое больше модуля первого перемещения. Движение на втором участке прямолинейное равномерное со скоростью υ2 = 20 м/с. Найти среднюю скорость перемещения и среднюю скорость на всем пути.

11. Линейная скорость точек обода вращающегося диска 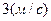, точек находящихся на 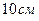ближе к оси вращения – 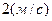. Найти угловую скорость.

12. Камень массой 300 г, привязанный к нити длиной 40 см, вращается в вертикальной плоскости вокруг оси, проходящей через другой конец нити. На какую высоту, отсчитываемую от нижней точки окружности поднимется камень, если нить оборвется в тот момент, когда скорость камня направлена вверх.

13. Шарик подвешенный на нити длиной 0,8 м описывает окружность в горизонтальной плоскости так, что нить образует угол 60° с вертикалью. Найти период обращения маятника.

14. Автомобиль мощностью N 1 развивает скорость υ1, а автомобиль мощностью N 2 развивает скорость υ2. Какую скорость разовьют эти автомобили, если их сцепить жестким тросом?

15. Вертолет начал снижаться с ускорением 0,2 м/с2. Лопасть винта вертолета имеет длину 5 м и совершает 300 об/мин. Определите число оборотов лопасти за время снижения вертолета на 40 м, линейную скорость и центростремительное ускорение.

16. Во сколько раз надо изменить скорость тела, брошенного горизонтально, чтобы, при вдвое большей высоте, с которой оно брошено, получить прежнюю дальность полета? Сопротивлением воздуха пренебречь.

17. Маховик радиусом 1 м начинает вращаться равноускоренно. Через 6 с точка, лежащая на его ободе, приобретает линейную скорость 20 м/с. Найти линейную скорость, тангенциальное, центростремительное и полное ускорения этой точки через 30 с от начала движения.


18. С балкона находящегося на высоте 10 м от поверхности Земли бросили камень вверх под углом 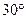к горизонту со скоростью 10 м/c. Определить время падения, дальность полета и скорость, с которой камень упадет на Землю.

19. Камень бросили с вышки в горизонтальном направлении с начальной скоростью 30 м/c. Определить скорость, касательное и центростремительное ускорение камня через две секунды после начала движения.

20. После удара тело движется вверх по наклонной плоскости с углом наклона 45º к горизонту. Остановившись оно соскальзывает назад вниз. Определить коэффициент трения о плоскость, если время спуска тела в два раза больше времени его подъема.

21. Невесомый блок укреплен на вершине наклонной плоскости с углом наклона 30° к горизонту. Два груза соединены нитью. Нить перекинута через блок так, что груз массой 2 кг находится на наклонной плоскости, а груз массой 1 кг свободно свисает. Найти силу натяжения нити, силу давления на блок. Трением пренебречь.

22. Груз массой 100 кг перемещают равномерно по горизонтальной поверхности, прилагая силу, направленную под углом 300 к горизонту. Определить величину этой силы, если коэффициент трения скольжения равен 0,3.

23. По наклонной плоскости, составляющей с горизонтом угол α, движется груз массой m, к которому приложена сила , направленная под углом β к наклонной плоскости. Коэффициент трения скольжения равен k. Найти ускорение тела.

24. Шар на нитке подвешен к потолку трамвайного вагона. Вагон тормозится и его скорость за 3с равномерно уменьшается от 18 км/ч до 6 км/ч. На какой угол отклонится при этом нить с шаром?

25. Какой массы mx, балласт надо сбросить с равномерно опускающегося аэростата, чтобы он начал равномерно подниматься с той же скоростью? Масса аэростата с балластом 1600 кг, подъемная сила аэростата 12 кН. Считать силу сопротивления Fсопр воздуха одной и той же при подъеме и спуске.

26. Диск вращается вокруг вертикальной оси с частотой 30 об/мин. На расстоянии 20 см от оси вращения на диске лежит тело. Каким должен быть коэффициент трения k между телом и диском, чтобы тело не скатывалось с диска?

27. К концам легкой нерастяжимой нити, перекинутой через неподвижный блок, подвешены грузы массами m 1 и m 2. Определите ускорение движения грузов и силу натяжения нити. Массой блока и силами трения можно пренебречь.

28. По наклонной плоскости, расположенной под углом 300 к горизонту, скользит тело. Найти его ускорение, если коэффициент трения 0,3.

29. Вагонетку массой 3 т поднимают по рельсам в гору, наклон которой к горизонту составляет 300. Какую работу совершает сила тяги на пути 50 м, если известно, что вагонетка двигалась с ускорением 0,2 м/с2, а коэффициент трения равен 0,1.


30. Конькобежец массой 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой 3 кг со скоростью 8 м/с относительно Земли. Найти, на какое расстояние откатится при этом конькобежец, если коэффициент трения коньков о лед равен 0,02.

31. Человек массой 70 кг поднимается в лифте. Лифт перед остановкой движется равнозамедленно вертикально вверх с ускорением 1 м/с2. Определите вес человека в лифте.

32. Груз массой 3 т поднимается лебедкой с ускорением 2 м/с2. Определить работу, произведенную в первые 1,5 сек от начала подъема.

33. Какую силу F надо приложить к вагону, стоящему на рельсах, чтобы вагон стал двигаться равноускоренно и за 30 с прошел путь 11 м? Масса вагона 16 тонн. Во время движения на вагон действует сила трения Fтр, равная 0,05 действующей на него силы тяжести mg.

34. При расследовании причин ДТП необходимо определить, возможно ли движение автомобиля вверх по горной дороге с уклоном, равным 300, с ускорением 0,6 м/с2, если коэффициент трения между шинами и поверхностью дороги 0,5.

35. К нити подвешена гиря. Если поднимать гирю с ускорением 2 м/с2, то сила натяжения нити Т 1 будет вдвое меньше той силы натяжения Т 2, при которой нить разорвется. С каким ускорением а 2 надо поднимать гирю, чтобы нить разорвалась?

36. Автомобиль массой 1020 кг, двигаясь равнозамедленно, остановился через 5с, пройдя путь 25 м. Найти начальную скорость автомобиля υ0 и силу торможения F.

37. В цилиндрический сосуд налиты равные массы воды и ртути. Общая высота двух слоев жидкостей 30 см. Определите давление жидкостей на дно.

38. Определить давление р воды на стенку цилиндрического сосуда с диаметром основания 20 см на расстоянии 5 см от дна. Объем воды в сосуде 10 л, плотность воды 103 кг/м3.

39. Давление воздуха в сосуде с отверстием, закрытым круглой пробкой диаметром 4 см, превышает атмосферное давление в 5 раз. Найти атмосферное давление ратм, если для того, чтобы удержать пробку, необходимо к ней приложить минимальную силу 510 Н.

40. Цилиндрический сосуд с диаметром основания, равным высоте цилиндра, наполнен доверху водой. Найти разность ∆ F сил давления воды на дно и стенку цилиндра. Плотность воды 103 кг/м3, высота цилиндра 20 см.

41. В двух цилиндрических сообщающихся сосудах налита ртуть. Сечение одного из сосудов вдвое больше другого. Широкий сосуд доливают водой до края. На какую высоту h поднимается при этом уровень ртути в другом сосуде? Первоначально уровень ртути был на расстоянии l от поверхности края широкого сосуда. Плотность ртути ρ, воды ρ 0.

42. При подъеме груза массой М с помощью гидравлического пресса была затрачена работа А (только на перемещение малого поршня). При этом малый поршень сделал n ходов, перемещаясь за один ход на расстояние h. Во сколько раз площадь большего поршня больше площади малого?

43. В цилиндрических сообщающихся сосудах с одинаковыми диаметрами и одинаковой высотой находится ртуть. В одном из сосудов поверх ртути налит столб воды высотой 32 см. Как будут расположены друг относительно друга уровни ртути в обоих сосудах, если оба они будут доверху залиты керосином?

44. Полый цинковый шар, наружный объем которого 200 см3, плавает в воде так, что половина его погружена в воду. Найти объем полости шара. Плотность воды 103 кг/м3, плотность цинка – 7,1·103 кг/м3.

45. До какой высоты h нужно налить однородную жидкость в цилиндрический сосуд радиусом R, чтобы силы, с которой жидкость будет давить на боковую поверхность, была равна силе давления на дно сосуда?

46. На какой угол повернется карусель после начала действия постоянного тормозящего момента М = 2·103 Н·м, если она вращалась, делая 0,5 оборота за секунду? Момент инерции карусели относительно оси I = 500 кг·м2.

47. На барабан массой m 0 = 9 кг намотан шнур, к концу которого привязан груз массой m = 2 кг. Найти ускорение груза. Барабан считать однородным цилиндром. Трением пренебречь.

48. Найти относительную ошибку δ, которая получится при вычислении кинетической энергии катящегося шара, если не учитывать вращение шара.

49. Карандаш длиной l = 15 см поставлен вертикально, падает на стол. Какую угловую скорость ω и линейную скорость υ будет иметь в конце падения середина и верхний конец карандаша?

50. Найти момент инерции I и момент импульса L земного шара относительно оси вращения.

51. Однородный стержень длиной l = 1 м и массой m = 0,5 кг вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через середину стержня. С каким угловым ускорением ε вращается стержень, если на него действует момент сил М = 98,1 мН·м?

52. Маховик, момент инерции которого I = 63,6 кг·м2 вращается с угловой скоростью ω = 31,4 рад/с. Найти момент сил торможения М, под действием которого маховик останавливается через время t = 20 с. Маховик считать однородным диском.

53. Маховик радиусом R = 0,2 м и массой m = 10 кг соединен с мотором при помощи приводного ремня. Сила натяжения ремня, идущего без скольжения Т = 14,7 Н. Какую частоту вращения n будет иметь маховик через время t = 10 с после начала движения? Маховик считать однородным диском. Трением пренебречь.

54. К ободу колеса радиусом R = 0,5 м и массой m = 50 кг приложена касательная сила F = 98,1 Н. Найти угловое ускорение ε колеса.

55. Шар диаметром d = 6 см и массой m = 0,25 кг катится без скольжения по горизонтальной плоскости с частотой вращения n = 4 об/с. Найти кинетическую энергию шара.

56. Диск диаметром d = 60 см и массой m = 1 кг вращается вокруг оси, проходящей через центр перпендикулярно к его плоскости с частотой n = 20 об/с. Какую работу надо совершить, чтобы остановить диск?

57. Мальчик катит обруч по горизонтальной дороге со скоростью υ = 7,2 км/ч. На какое расстояние s может вкатиться обруч на горку за счет его кинетической энергии? Уклон горки равен h = 10 м на каждые l = 100 м пути.

58. Ведерко с водой, привязанное к веревке длинной l = 60 см, равномерно вращается в вертикальной плоскости. Найти наименьшую скорость υ вращения ведерка, при которой в высшей точке вода из него не выливается. Какова сила натяжения веревки Т при этой скорости в высшей и низшей точках окружности? Масса ведерка с водой m = 2 кг.

59. Сплошной однородный цилиндр массы m без проскальзывания катится по горизонтальной поверхности так, что его ось перемещается со скоростью υ. Радиус цилиндра r. Найти кинетическую энергию цилиндра относительно горизонтальной плоскости.

60. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой n = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения М тр и время t, прошедшее от момента прекращения действия вращающего момента до остановки колеса.

61. К ободу диска массой m = 5 кг приложена касательная сила F = 19,6 Н. Какую кинетическую энергию W кбудет иметь диск через время t = 5 с, после начала действия силы?

62. Обруч диаметром d = 56,5 см висит на гвозде, вбитом в стенку, и совершает малые колебания в плоскости параллельной стене. Найти период колебаний Т обруча.

63. Чему равен момент инерции цилиндра I с диаметром основания d и высотой h относительно оси О1О2, совпадающей с его образующей? Плотность материала цилиндра ρ.

64. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы с частотой n 1 = 10 об/мин. Человек массой m 0 = 60 кг стоит при этом на краю платформы. С какой частотой n 2 начнет вращаться платформа, если человек перейдет от края платформы к её центру? Считать платформу однородным диском, а человека – точечной массой.

65. Кинетическая энергия вала, вращающегося с частотой n = 5 об/с, Е к = 60 Дж. Найти момент импульса вала.

66. На гладкой горизонтальной поверхности лежит невесомый стержень длиной l с надетыми на его концы маленькими шариками массой m и 2 m. На шарик массой m налетает со скоростью υ 0 материальная точка массой m 0 и прилипает к нему. С какой скоростью υ c станет двигаться центр масс С стержня, если вектор скорости материальной точки направлен под углом 900 к стержню.

67. Подъемный кран поднимает в течение времени t = 2 мин стальную плиту со скоростью υ = 0,5 м/с. Длина плиты l = 4 м, ширина r = 50 см, высота h = 40 см. Какую полезную работу А совершает кран? Плотность стали ρ = 7,8·103 кг/м3.

68. Определить КПД водонапорной установки, если бак водоизмещением 40 м3, поднятый на высоту 10 м, наполняется водой за 12 минут насосом с электроприводом мощностью 7·103 Вт.

69. Пуля массой m 1 = 10 г, летевшая горизонтально со скоростью υ = 600 м/с, ударилась в свободно подвешенный на длинной нити деревянный брусок массой m 2 = 0,5 кг и застряла в нём, углубившись на h = 10 см. Найти силу сопротивления F дерева движению пули.

70. Вычислить мощность двигателя подъемного крана, поднимающего груз массой m = 3 т с постоянной скоростью υ = 6 м/мин, если КПД крана 80%.

71. Шарик массой m, движущейся со скоростью υ 1, упруго ударяется о гладкую стенку под углом α к ней и отскакивает без потери скорости. Определить изменение импульса шарика. Чему равна средняя сила, действующая на шарик со стороны стенки, если продолжительность удара ∆ t?

72. Тело соскальзывает без трения по наклонному желобу и описывает мертвую петлю радиуса R. Какой должна быть минимальная высота желоба H, чтобы тело проходило верхнюю точку петли не отрываясь?

73. Мяч, летящий со скоростью υ 1 = 15 м/с, отбрасывается ударом ракетки в противоположном направлении со скоростью υ 2 = 20 м/с. Найти изменение импульса m ∆ υ мяча, если известно, что изменение его кинетической энергии ∆ W = 8,75 Дж.

74. Найти работу А, которую надо совершить, чтобы увеличить скорость движения тела массой m = 1 т от υ 1 = 2 м/с до υ 2 = 6 м/с на пути s = 10 м. На всем пути действует сила трения F = 2 Н.

75. Тело массой m 1 = 1 кг, движущееся горизонтально со скоростью υ 1 = 1 м/с, догоняет второе тело массой m 2 = 0,5 кг и неупруго соударяется с ним. Какую скорость u получат тела, если а) второе тело стояло неподвижно; б) второе тело двигалось со скоростью υ 2 = 0,5 м/с в направлении, что и первое тело; в) второе тело двигалось со скоростью υ 2 = 0,5 м/с в направлении, противоположном направлению движения первого тела.

76. Два тела движутся навстречу друг другу и соударяются неупруго. Скорости тел до удара были υ 1 = 2 м/с и υ 2 = 4 м/с. Общая скорость тел после удара u = 1 м/с и по направлению совпадает с направлением скорости υ 1. Во сколько раз кинетическая энергия W к1 первого тела была больше кинетической энергии W к2 второго тела?

77. К нити подвешена гиря. Если поднимать гирю с ускорением а 1 = 2 м/с2, то сила натяжения Т 1 будет вдвое меньше той силы натяжения Т 2, при которой нить разорвется. С каким ускорением а 2 надо поднимать гирю, чтобы нить разорвалась?

78. Граната, летевшая со скоростью υ = 15 м/с, разорвалась на две части с массами m 1 = 6 кг и m 2 = 14 кг. Скорость большого осколка υ 2 = 24 м/с направлена так же, как и скорость гранаты до взрыва. Найти направление и абсолютную величину скорости меньшего осколка.

79. Пуля вылетает из винтовки со скоростью υ п = 900 м/с. Найти скорость винтовки при отдаче, если её масса m в в 500 раз больше массы пули m п.

80. Груз массой m = 3 т поднимается лебедкой с ускорением a = 2 м/с2. Определить работу, произведенную в первые 1,5 с от начала подъема.

81. В кислородной подушке вместимостью 1 л содержится 12 кг кислорода. Найти давление кислорода при 150С. Плотность кислорода при н.у. 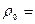1,43 кг/м3.

82. Определите коэффициент теплопроводности 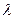азота, находящегося в некотором объеме при температуре 280 К. Эффективный диаметр молекул азота примите равным 0,38 нм.

83. Углекислый газ массой 6,6 кг при давлении 0,1 МПа занимает объем 3,75 м3. Определите температуру газа, если: 1) газ реальный; 2) газ идеальный. Поправки a и b примите равными соответственно 0,361 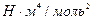и 4,28

84. Для получения низких температур производят адиабатическое расширение гелия, имеющего первоначальную температуру 300 К и объем 10 л. При этом давление падает от 5МПа до 0,2 МПа. Найти объем и температуру гелия в конечном состоянии. Для гелия показатель адиабаты 1,66.

85. В озере на глубине 100 м при температуре 80С находится в равновесии шар массой 40 г, наполненный воздухом. Найти массу воздуха внутри шара, если атмосферное давление 99,7 кПа. Шар считать тонкостенным, изготовленным из резины.

86. Баллон содержит водород массой 10 г при температуре 280 К. Определить кинетическую энергию всех молекул газа.

87. Из баллона со сжатым водородом вместимостью 10 л вследствие неисправности вентиля утекает газ. При 70С манометр показывает давление 5 МПа. Показание манометра не изменилось и при 170С. Определить массу вытекшего газа.

88. Если бы все молекулы водорода, содержащиеся в m = 10 мг этого газа, расположили вплотную друг к дружке по цепочке, то какова была бы длина этой цепочки? Диаметр молекулы водорода d = 2,3 Å, молярная масса водорода М = 2·10-3 кг/моль. Во сколько раз длина этой цепочки больше расстояния от Земли до Луны L = 384 Мм? (1 Å = 10-10 м).

89. На изделие, имеющее форму круглой пластинки диаметром d = 2 см, нанесен слой меди толщиной h = 2 мкм. Найти число атомов меди N, содержащихся в этом покрытии. Плотность меди ρ = 8,9·103 кг/м3, молярная масса меди М = 0,064 кг/моль.

90. Определить плотность смеси, содержащей m 1 = 4 г водорода и m 2 = 32 г кислорода при t = 7 °С и общем давлении p = 105 Па.

91. В бассейн длиной 10 м, шириной 6 м и глубиной 2 м бросили 10 г поваренной соли. Соль равномерно распределилась по всему объему бассейна. Найти количество молекул N соли в стакане объемом 200 см3, которым зачерпнули воду из бассейна. Молярная масса соли NaCl 58·10-3 кг/моль.

92. Давление газа 100 кПа, а средняя квадратичная скорость его молекул 400 м/с. Найти его плотность.

93. В результате нагревания давление газа в закрытом сосуде увеличилась N раз. Во сколько раз увеличилась средняя квадратичная скорость его молекул?

94. В цилиндре под поршнем находится углекислый газ массой 0,2 кг. Газ нагревается на 88 К. Какую работу А он при этом совершает?

95. Объем 7,5 л кислорода адиабатически сжимается до 1 л, причем в конце сжатия давление установилось 1,6 МПа. Под каким давлением газ находится до сжатия?

96. Какую температуру имеет масса m = 2 г азота, занимающего объем 820 см3 при давлении р = 0,2 МПа?

97. В сварочном цехе стоит 30 баллонов ацетилена вместимостью 40 л каждый. Все баллоны включены в общую магистраль. После 12 часов непрерывной работы давление упало с 13 до 7 атм. Найти расход ацетилена за 1 с, если постоянная температура равна 32 °С. Молярная масса ацетилена 26·10–3 кг/моль. (Газ считать идеальным).

98. В процессе нагревания газа в цилиндре передано количество теплоты 1,5·105 Дж, причем давление газа оставалось постоянным и равным 2·107 Па. Площадь сечения цилиндра 200 cм2, поршень передвинулся на 30 см. На сколько изменилась внутренняя энергия газа?

99. Найти для углекислого газа 1) массу одной молекулы, 2) число молекул, содержащихся в единице массы, 3) число молекул в 1м3 при нормальных условиях.

100. Газообразный азот массой 14 г, находящийся при температуре 27°С, изохорно охлаждается так, что давление уменьшается в три раза. Затем газ изобарно нагревается до первоначальной температуры. Определить произведенную газом работу.

101. Оцените радиус атома меди R, приняв, что в твердом состоянии меди ее атомы располагаются вплотную друг к другу. Плотность меди 8,9·103 кг/м3, её молярная масса 0,064 кг/моль.

102. Для получения хорошего вакуума в стеклянном сосуде необходимо подогревать стенки сосуда при откачке для удаления адсорбированного газа. На сколько может повыситься давление в сферическом сосуде радиусом r = 10 см, если адсорби­рованные молекулы перейдут со стенок в сосуд? Площадь поперечного сечения молекул s 0 = 10-19 м2. Температура газа в сосуде t = 300 °С. Слой молекул на стенках считать мономолекулярным.

103. Найти массу m воздуха, заполняющего аудиторию высотой 5 м и площадью пола 200 м2. Давление воздуха 100 кПа, температура помещения 17 °С. Молярная масса воздуха 0,029 кг/моль.

104. Найти число молекул газа N, средняя квадратичная скорость которых при температуре 27 0C 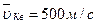, если масса газа 10 г.

105. Во сколько раз плотность воздуха ρ1, заполняющего помещение зимой (t = 7 0С), больше его плотности ρ2 летом (t = 37 0С)? Давление газа считать постоянным.

106. Воздух представляет смесь газов. Пусть на уровне земли отношение концентраций кислорода и азота равно 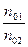. Используя распределение Больцмана определить отношение концентраций этих газов на высоте 1000 м. Температуру на уровне земли и на высоте h считать одинаковой и равной 273 К.

107. Газ расширяется адиабатически, причем объем его увеличивается вдвое, а термодинамическая температура падает в 1,32 раза. Какое число степеней свободы i имеют молекулы?

108. Какая доля молекул кислорода при температуре 300 К имеет скорость в интервале от (υв – 1) м/с до (υв + 1) м/с? Молярная масса кислорода 0,032 кг/моль.

109. Найти энергию вращательного движения молекул, содержащихся в массе 1 кг азота при температуре 7 °С.

110. Давление воздуха внутри плотно закупоренной бутылки при температуре 7 0С было 100 кПа. При нагревании бутылки пробка вылетела. До какой температуры t2 нагрели бутылку, если известно, что пробка вылетела при давлении воздуха в бутылке 130 кПа.

111. В цилиндре под поршнем находится воздух. Вес поршня 60 Н, площадь сечения цилиндра 20 см2, атмосферное давление p0 = 105 Па. Груз какого веса надо положить на поршень, чтобы объем воздуха в цилиндре уменьшился в 2 раза? Температуру считать постоянной, трение не учитывать. Масса воздуха не изменяется.

112. Гелий имеет плотность 0,12 кг/м3 при давлении 100 кПа. Найти среднюю кинетическую энергию поступательного движения одной молекулы гелия. Молярная масса гелия 4·10–3 кг/моль.

113. Какое число молекул находится в комнате объемом V = 80 м3 при температуре t = 17 0С и давлении р = 100 кПа?

114. Какой объем занимает масса 10 г кислорода при давлении 100 кПа и температуре 20 0С?

115. В запаянном сосуде находится вода, занимающая объем, равный половине объема сосуда. Найти давление р и плотность ρ водяного пара при температуре 400 °С, зная, что при этой температуре вся вода обращается в пар.

116. При изобарическом расширении двухатомного газа была совершена работа 156,8 Дж. Какое количество теплоты было сообщено газу?

117. Масса 6,5 г водорода, находящегося при темпе­ратуре 27 °С, расширяется вдвое при р = const за счет при­тока тепла извне. Найти работу расширения газа, изменение внутренний энергии газа и количество теплоты, сообщенное газу.

118. Закрытый сосуд объемом 2л наполнен воздухом при нормальных условиях. В сосуд вводится диэтиловый эфир (С2Н5ОС2Н5). После того как весь эфир испарился, давление в сосуде стало равным 0,14 МПа. Какая масса m эфира была введена в сосуд?

119. Массу 5 г азота, находящегося в закрытом сосуде объемом 4 л при температуре 20 0С нагревают до температуры 40 0С. Найти давление газа до и после нагревания.

120. Идеальная тепловая машина, работающая по циклу Карно, за цикл получает от нагревателя количество теплоты 2.512 кДж. Температура нагревателя 400 0С, температура холодильника 300 0С. Найти работу, совершаемую машиной за один цикл, и количество теплоты, отдаваемое холодильнику за один цикл.

 

КОНТРОЛЬНАЯ РАБОТА №2

1. Электрон движется без начальной скорости вдоль силовой линии однородного электрического поля напряженностью E = 2·104 Н/Кл. Какой путь S он пролетит прежде, чем его скорость станет υ = 100 км/с? Среда – воздух.

2. Сколько электронов находится на пылинке массой m = 10–11 г, если она удерживается между двумя параллельными пластинками. Расстояние между пластинками d = 5 мм, разность потенциалов U = 76,5 В. С каким ускорением a и в какую сторону будет двигаться пылинка, если она лишится N = 20 электронов?

3. Электрон влетает в однородное электрическое поле со скоростью
υ = 1,8∙103 км/с и движется по направлению силовых линий. Напряженность поля равна E = 90 В/м. Через сколько времени t скорость электрона станет равной нулю?

4. Пучок электронов, движущихся с классической скоростью, падает на металлический изолированный шар, диаметром D. Какое максимальное число электронов N может накопиться на шаре?

5. Два точечных заряда, находясь в воздухе (ε = 1) на расстоянии r 1 = 20 см друг от друга взаимодействуют с некоторой силой. На каком расстоянии r 2 нужно поместить эти заряды в масле (ε = 5), чтобы получить туже силу взаимодействия?

6. С какой силой F s на единицу площади отталкиваются две одноименно заряженные плоскости? Поверхностная плотность заряда на плоскостях σ = 0,3 мКл/м2.

7. Медный шар радиусом R = 0,5 см помещен в масло. Плотность шара ρ = 0,8 кг/м3. Найти заряд шара q, если в однородном электрическом поле шар оказался взвешенным в масле. Электрическое поле направлено вертикально вверх и его напряженность Е = 3,6 МэВ.

8. Два заряженных шарика, подвешенных на нитях одинаковой длины, опускаются в керосин плотностью ρ = 0,8 кг/м3. Какой должна быть плотность материала шариков, чтобы угол расхождения нитей в воздухе и в керосине был один и тот же? Диэлектрическая проницаемость керосина ε = 2.

9. В плоском горизонтально расположенном конденсаторе заряженная капелька ртути находится в равновесии при напряженности электрического поля Е = 60 кВ/м, заряд капли q = СГСq. Найти радиус капли.

10. При изучении фотоэлектрических явлений используется сферический конденсатор, состоящий из металлического шарика диаметром d = 1,5 см и внутренней поверхности посеребренной изнутри сферической колбы диаметром D = 11 см. Воздух из колбы откачивается. Найти ёмкость C такого конденсатора.

11. При помощи электрометра сравнивали между собой емкости двух конденсаторов. Для этого их заряжали до разности потенциалов U 1 = 300 В и U 2 = 100 В и соединяли оба конденсатора параллельно. Измеренная при этом электрометром разность потенциалов между обкладками конденсатора оказалась равной U = 250 В. Найти соотношение емкостей C 1/ С 2.

12. Шар радиусом R = 1 м заряжается до потенциала φ = 30 кВ. Найти энергию заряженного шара.

13. Между пластинками плоского конденсатора вложена тонкая слюдяная пластинка. Какое давление р испытывает эта пластинка при напряженности поля Е = 1 МВ·м?

14. Площадь пластин плоского воздушного конденсатора S = 0,01 м2, расстояние между ними d = 5 мм. Какая разность потенциалов U была приложена к пластинам конденсатора, если известно, что при разряде конденсатора выделилось Q = 4,19 мДж тепла?

15. Воздушный конденсатор емкостью С 1 = 10–9 Ф зарядили до напряжения U 1 = 600 В. Затем, отключив от источника, раздвинули пластины, увеличив расстояние между ними в 2 раза. Определите конечное напряжение U 2, заряд q 2 и работу А, которую надо совершить для увеличения расстояния между обкладками.

16. Как изменится емкость плоского воздушного конденсатора, пластины которого расположены вертикально, если конденсатор погрузить до половины в жидкий диэлектрик с относительной диэлектрической проницаемостью равной 5?

17. Плоский воздушный конденсатор зарядили до разности потенциалов U 1 = 600 В, а затем отключили от источника тока. Какой станет разность потенциалов U 2 между пластинами, если расстояние между ними увеличить от d 1 = 0,2 мм до d 2 = 0,7 мм, и, кроме того, пространство между пластинами заполнить слюдой с диэлектрической проницаемостью ε 2 = 7?

18. Поверхностная плотность зарядов на обкладках плоского воздушного конденсатора σ = 0,1 мкКл/м2, площадь обкладок S = 5 см2, ёмкость конденсатора С = 1 пФ. Какую скорость v приобретет электрон, пройдя по силовой линии расстояние от одной обкладки до другой, если его начальная скорость υ 0 = 0?

19. При увеличении напряжения на конденсаторе в 3 раза энергия поля между его обкладками увеличилась на ∆ W = 200 мДж. Найти начальную энергию конденсатора W 1.

20. Воздушный конденсатор с зарядом на обкладках q, площадью обкладок S и расстоянием между ними d погружают в жидкость с диэлектрической проницаемостью 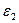на ¼ его объема. Найти напряжение на обкладках конденсатора после погружения.

21. Найти количество теплоты Q, выделившееся при соединении одноименно заряженных обкладок конденсаторов с емкостями С 1 = 2 мкФ и С 2 = 0,5 мкФ. Напряжения на конденсаторах до соединения были соответственно U 1 =100 В и U 2 =50 В.

22. Два шарика с зарядами q 1 = 6,66 нКл и q 2 = 13,33 нКл находятся на расстоянии r 1 = 40 см. Какую работу А надо совершить, чтобы сблизить их до расстояния r 2 = 25 см?

23. Найти потенциал φ точки поля, находящейся на расстоянии r = 10 см от центра заряженного шара радиусом R = 1 см. Поверхностная плотность заряда σ = 0,1 мкКл/м2.

24. Какая работа А совершается при пересечении точечного заряда q = 20 нКл из бесконечности в точку, находящуюся на расстоянии r = 1 см от поверхности шара радиусом R = 1 см с поверхностной плотностью заряда σ = 10 мкКл/м2?

25. Шарик массой m = 1г и зарядом q = 10 нКл перемещается из точки 1, потенциал которой φ 1 = 600 В, в точку 2, потенциал которой φ 2 = 0. Найти его скорость υ 1 в точке 1, если в точке 2 она стала υ 2 = 20 см/с.

26. Около заряженной бесконечно протяженной плоскости находится заряд q = 0,66 нКл. Заряд перемещается по линии напряженности поля на расстояние ∆ r = 2 см, при этом совершается работа А = 50 эрг. Найти поверхностную плотность заряда σ на плоскости.

27. Найти отношение между радиусом R шара и максимальным потенциалом φ, до которого он может быть заряжен в воздухе, если при нормальном давлении разряд в воздухе наступает при напряженности электрического поля Е 0 = 3 МВ/м. Каким будет максимальный потенциал φ шара диаметром D = 1 м?

28. В медном проводнике сечением S = 6 мм2 и длиной l = 5 м течет ток. За t = 1 мин в проводнике выделяется Q = 18 Дж теплоты. Определить напряженность поля E, плотность j и силу I электрического тока в проводнике.

29. Определить плотность j электрического тока в медном проводе (удельное сопротивление ρ = 17 нОм·м), если удельная тепловая мощность тока w = 1,7 Дж/(м3·с).

30. Внутреннее сопротивление аккумулятора r = 2 Ом. При замыкании его одним резистором сила тока равна I 1 = 4 А, при замыкании другим I 2 = 2 А. Во внешней цепи в обоих случаях выделяется одинаковая мощность. Определить электродвижущую силу аккумулятора и внешние сопротивления R 1, R 2.

31. Гальванический элемент замыкается один раз на сопротивление R 1 = 9 Ом, другой раз на R 2 = 4 Ом. В том и другом случаях количество теплоты Q, выделяющееся в сопротивлениях за одно и то же время, оказывается одинаковым. Каково внутреннее сопротивление r элемента?

32. Найти ЭДС и внутреннее сопротивление источника тока, если при сопротивлении нагрузки R 1 = 2 Ом сила тока в цепи I 1 = 0,4 A, а при R 2 = 1,5 Ом I 2 = 0,6 А. Чему равна сила тока короткого замыкания I КЗ?

33. Определить внутреннее r сопротивление источника тока, если во внешней цепи при силе тока I 1 = 4 А развивается мощность P 1 = 10 Вт, а при силе тока I 2 = 6 А – мощность P 2 = 12 Вт.

34. ЭДС батареи равна 20 В. Коэффициент полезного действия батареи при силе тока I = 4 А, составляет η = 0,8. Чему равно внутреннее сопротивление r батареи?

35. Вольфрамовая нить электрической лампочки при t 1 = 20 0С имеет сопротивление R 1 = 35,8 Ом. Какова будет температура t 2 нити лампочки, если при включении в сеть напряжением U = 120 В по нити идет ток I = 0,33 А? Температурный коэффициент сопротивления вольфрама α = 4,6·10-3К-1.

36. Реостат из железной проволоки, амперметр и генератор подключены последовательно. При t 0 = 0 0С сопротивление реостата R 0 = 120 Ом, сопротивление амперметра R A0 = 20 Ом. Амперметр показывает ток I 0 = 22 мА. Какой ток I будет показывать амперметр, если реостат нагревается на ∆ Т = 50 К? Температурный коэффициент сопротивления железа α = 6,0·10-3К-1.

37. Обмотка катушки из медной проволоки при t 1=14 0С имеет сопротивление R 1=10 Ом. После пропускания тока сопротивление обмотки стало равным R 2=12,2 Ом. До какой температуры нагрелась обмотка? Температурный коэффициент сопротивления меди α = 4,3·10-3К-1.

38. Найти падение потенциала U на медном проводе длиной l = 500 м и диаметром d = 2 мм, если ток в нем I = 2 А.

39. Элемент, имеющий ЭДС 1,1 В и внутреннее сопротивление r = 1 Ом, замкнут на внешнее сопротивление R = 9 Ом. Найти ток I в цепи, падение потенциала U во внешней цепи и падение потенциала U r внутри элемента. С каким КПД работает элемент?

40. Элемент с ЭДС 2 В имеет внутреннее сопротивление r = 0,5 Ом. Найти падение потенциала U r внутри элемента при токе в цепи I = 0,25 А. Каково внешнее сопротивление цепи R при этих условиях?

41. Элемент, сопротивление и амперметр соединены последовательно. Элемент имеет ЭДС 2 В и внутреннее сопротивление r = 0,4 Ом. Амперметр показывает ток I = 1 А. С каким КПД работает элемент?

42.

43. Имеются три 110-вольтовых электрических лампочки, мощности которых P 1 = P 2 = 40Вт. Как надо включить эти лампочки, чтобы они давали нормальный накал при напряжении в сети U 0 = 220 В? Начертить схему. Найти токи I 1, I 2, I 3, текущие через лампочки при нормальном накале.

44. В лаборатории, удаленной от генератора на расстояние l = 100 м, включили электрический нагревательный прибор, потребляющий ток I = 10 А. На сколько понизилось напряжение на зажимах электрической лампочки, горящей в этой лаборатории, если сечение медных проводящих проводов S = 5 мм2?

45. От батареи с ЭДС 500 В требуется передать энергию на расстояние l = 2,5 км. Потребляемая мощность Р = 10 кВт. Найти минимальные потери мощности ∆Р в сети, если диаметр медных проводящих проводов d = 1,5 см.

46. От генератора с ЭДС 110 В требуется передать энергию на расстояние l = 250 м. Потребляемая мощность Р = 1 кВт. Найти минимальное сечение S медных проводящих проводов, если потери мощности в сети не должны превышать 1%.

47. В цепь включены последовательно медная и стальная проволоки одинаковых длины и диаметра. Найти: 1) отношение количеств теплоты, выделяющихся в этих проволоках; 2) отношение падений напряжения на этих проволоках.

48. Элемент с ЭДС 6 В дает максимальный ток I = 3 А. Найти наибольшее количество теплоты Q r, которое может быть выделено во внешнем сопротивлении в единицу времени.

49. Две электрические лампочки с сопротивлениями R 1 = 360 Ом и R 2 = 240 Ом включены в сеть параллельно. Какая из лампочек потребляет большую мощность и во сколько раз?

50. Какой объем воды можно вскипятить, затратив электрическую энергию W = 3 гВт·ч? Начальная температура воды t 0 = 100С. Удельная теплоемкость воды с = 4,2·103 Дж/кг·К.

51. Какую мощность потребляет нагреватель электрического чайника, если объем V = 1 л воды закипает через время τ = 5 мин? Каково сопротивление R нагревателя, если напряжение в сети U = 120 В? Начальная температура воды t 0 = 13,5 0С. Удельная теплоемкость воды с = 4,2·103 Дж/кг·К.

52. Объем V = 4,5 л воды можно вскипятить, затратив электрическую энергию W = 0,5 кВт·ч. Начальная температура воды t = 23 0С. Найти КПД нагревателя.

53. Температура водяного термостата объемом V = 1 л поддерживается постоянной при помощи нагревателя мощностью Р = 26 Вт. На нагревание воды тратится 80 % этой мощности. На сколько понизится температура воды в термостате за время τ = 10 мин, если нагреватель выключить? Удельная теплоемкость воды с = 4,2·103 Дж/кг·К.

54. Найти количество теплоты Q r, выделившееся в единицу времени в единице объема медного провода при плотности тока j = 300 кА/м2. Удельное сопротивление меди ρ = 0, 017 мкОм·м.

55. В ртутном диффузионном насосе в единицу времени испаряется масса m τ = 100г/мин ртути. Каково должно быть сопротивление R нагревателя насоса, если он включается в сеть напряжением U = 127 В? Удельная теплота парообразования ртути q = 296 кДж/кг.

56. Найти напряженность Н магнитного поля в центре кругового проволочного витка радиусом R = 1 см, по которому течет ток I = 1 А.

57. Два прямолинейных длинных проводника расположены параллельно на расстоянии d = 10 см друг от друга. По проводникам текут токи I 1 = I 2 = 5А в противоположных направлениях. Найти модуль и направление напряженности 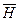магнитного поля в точке, находящейся на расстоянии а = 10 см от каждого проводника.

58. Ток I = 20 А, протекая по кольцу из медной проволоки сечением S = 1 мм2, создает в центре кольца напряженность магнитного поля Н = 178 А/м. Какая разница потенциалов U приложена к концам проволоки, образующей кольцо?

59. Найти напряженность Н магнитного поля на оси кругового контура на расстоянии а = 3 см от его плоскости. Радиус контура R = 4 см, ток в контуре I = 2 А.

60. По проводу, согнутому в виде квадрата со стороной a = 10 см, течет ток силой I = 100 А. Найти магнитную индукцию B в точке O пересечения диагоналей квадрата.

61. Проводник из металла длиной l = 1,5 м перемещается в магнитном поле индукции В = 0,2 Тл равномерно со скоростью υ = 3 м/с. Найти ЭДС индукции в проводнике, если линии магнитного поля перпендикулярны длине проводника и направлению его движения.

62. Два прямолинейных длинных параллельных проводника находятся на расстоянии d 1 = 10 см друг от друга. По проводникам в одном направлении текут токи I 1 = 20A и I 2 = 30 А. Какую работу А надо совершить, чтобы раздвинуть эти проводники до расстояния d = 20 см.

63. Под каким углом α должен упасть луч на плоское зеркало, чтобы угол между отраженным лучом и поверхностью зеркала был φ = 300.

64. Угловая высота Солнца над горизонтом φ 1 = 400. Под каким углом φ 2 к горизонту надо расположить плоское зеркало, чтобы отраженный луч направить вертикально вверх?

65. Высота Солнца над горизонтом φ = 300. Наблюдатель, стоя на берегу, видит изображение Солнца в воде. Наклонившись, он понижает уровень глаз на h = 10 см. На какое расстояние S приблизится при этом изображение Солнца к берегу?

66. Два плоских зеркала расположены под углом друг к другу. Точечный источник света поместили между ними и в результате получили N = 11 изображений этого источника в зеркалах. Чему равен угол φ между зеркалами?

67. На каком расстоянии от собирающей линзы с фокусным расстоянием 10 см нужно поставить предмет, для того чтобы получить действительное изображение с увеличением в 10 раз?

 

68. Луч падает на поверхность стекла под углом α 1 = 600. Под каким углом α 2он должен упасть на поверхность воды, чтобы угол преломления в стекле γ 1 был равен углу преломления в воде γ 2? Показатель преломления стекла n 1= 1,5, показатель преломления воды n 2 = 1,33.

69. На стеклянную пластинку падает луч света. Показатель преломления стекла n = 1,5. Определить угол падения луча, если угол между отраженным и преломленным лучами равен 90º.

70. Луч света падает на горизонтальную стеклянную пластинку и преломляется в ней под углом β 1. Сверху пластинки наливают слой жидкости. Определите новое значение угла преломления β 2 света в стекле.

71. Предмет расположен на расстоянии l от фокальной плоскости собирающей линзы, главное фокусное расстояние которой F. Определите линейное увеличение Г. Считать, что l< F.

72. На расстоянии 16 см одна от другой находятся две собирающие линзы. Фокусное расстояние линз равны: F 1 = 8 см, F 2 = 5 см. Предмет высотой 4 см находится на расстоянии 40 см от первой линзы. На каком расстоянии от второй линзы получится изображение? Определить высоту изображения.

73. Расстояние между предметом и его изображением в выпуклом зеркале l = 20 см, а уменьшение изображения Г = 0,5. Чему равны фокусное расстояние F и радиус кривизны R?

74. Под каким углом должен упасть луч на поверхность стекла, чтобы угол преломления γ был в 2 раза меньше угла падения? Показатель преломления стекла n = 1,5.

75. Чему равен угол падения α луча на поверхность алмаза, если он больше угла преломления γ на φ = 300? Абсолютный показатель преломления алмаза n = 2,42.

76. На дне пруда недалеко от берега лежит камень. Ребенок на берегу, прицепившись и стараясь попасть в камень палкой, двигает ее под углом φ = 300 к поверхности воды. Палка падает на дно пруда на расстоянии l = 10 см от камня. Чему равна глубина пруда h в этом месте? Показатель преломления воды n = 1,33. Сопротивлением воды движению палки пренебречь.

77. Какова истинная глубина H озера, если его кажущаяся глубина h = 1,5 м? Показатель преломления воды n = 1,33.

78. Радиус кривизны вогнутого зеркала R = 20 см. на расстоянии а 1 = 30 см от зеркала поставлен предмет высотой y 1 = 1 см. Найти высоту y2 изображения. Дать чертеж.

79. Найти число длин волн N монохроматического света, укладывающихся на отрезке l = 2м, если частота излу­чения ν = 600 ТГц.

80. На мыльную пленку с показателем преломления n = 1,33 падает белый свет под углом α = 30°. При какой наименьшей толщине h поверхность пленки, наблюдаемая в отраженном свете, будет окрашена в желтый цвет? Длина волны желтого света λ = 6·10-7 м.

81. Белый свет падает нормально на мыльную пленку с показателем преломления п. Найти толщину пленки, если в проходящем свете интерференционный максимум наблюдается на волне λ 1 а ближайший к нему минимум на волне λ 2.

82. Установка для наблюдения колец Ньютона освещается монохроматическим светом с длиной волны λ = 6·10-7 м. Найти разность ∆ r между радиусами светлых колец спорядковыми номерами k 1 = 3 и k 2 = 4. Радиус кривизны линзы R = 8 м. Наблюдение ведется в отраженном свете.

83. На круглое отверстие диаметром D = 8 мм падает нормально плоская монохроматическая волна с длинной волны λ = 5·10-7 м. Найти число зон Френеля N, укладывающихся в этом отверстии, если расстояние от отверстия до экрана r 0 = 2 м.

84. Дифракционная решетка имеет N 1 = 1500 штрихов. Можно ли с помощью этой решетки в спектре первого порядка разрешить две линии спектра с длинами волн λ 1 = 600 нм и λ 2 = 600,5 нм? Будет ли разрешать эти линии решетка такой же длины с числом штрихов N 2 = 500?

85. Какой должна быть длина дифракционной решетки l, имеющей N = 800 штрихов на длине l 1 = 2 мм, чтобы с её помощью можно было разрешить в спектре второго порядка две линии спектра с длинами волн λ 1 = 500 нм и λ 2 = 500,02 нм?

86. Дифракционная решетка имеет N = 400 штрихов на длине l = 2 мм. Она расположена на расстоянии L = 1 м от экрана. На решетку падает белый свет с длиной волны красного цвета λ 1 = 720 нм и длиной волны фиолетового цвета λ 2 = 430 нм (рис. 58). Найти длину х спектра первого порядка на экране.

87. Дифракционная решетка имеет 500 штрихов на 1 мм, длина волны падающего света 540 нм. Определить период решетки и наибольший порядок спектра, который можно наблюдать с помощью этой дифракционной решетки. Чему равен максимальный угол дифракции для данной длины волны?

88. Расстояние между двумя мнимыми изображениями источника света в бипризме Френеля – 0,3 см. Что будет наблюдаться в точке экрана, удаленной на расстояние 9 м: максимум или минимум? Длина волны источника света l = 5·10 -7 м.

89. Определить угол отклонения луча стеклянной призмой (рис. 59), преломляющий угол которой 30 (0,052 рад), если угол падения луча на переднюю грань призмы равен нулю.

90. На стеклянную трехгранную призму (рис. 60) с преломляющим углом 450 (0,79 рад) падает


⇐ Предыдущая36373839404142434445





Date: 2015-08-15; view: 1494; Нарушение авторских прав


mydocx.ru - 2015-2024 year. (0.129 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию