
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Волновые свойства частиц. где р – импульс частицы
|
|
· Длина волны де Бройля
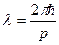 ,
,
где р – импульс частицы.
· Импульс частицы и его связь с кинетической энергией
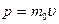 , или
, или  ,
,
где m 0 – масса покоя частицы; υ – скорость частицы; Е к – кинетическая энергия частицы.
· Соотношение неопределенностей Гейзенберга
1) Для координаты и импульса
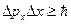 ,
,
где  – неопределенность проекции импульса на ось Х;
– неопределенность проекции импульса на ось Х;  – неопределенность координаты.
– неопределенность координаты.
2) Для энергии и времени  ,
,
где  – неопределенность энергии;
– неопределенность энергии;  – время жизни квантовой системы в данном энергетическом состоянии.
– время жизни квантовой системы в данном энергетическом состоянии.
· Одномерное уравнение Шредингера для стационарных состояний
 ,
,
где ψ – волновая функция, описывающая состояние частицы; m масса частицы; Е – полная энергия; U = U (x) – потенциальная энергия частицы.
· Плотность вероятности
 ,
,
где 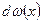 – вероятность того, что частица может быть обнаружена вблизи точки с координатой х на участке d x.
– вероятность того, что частица может быть обнаружена вблизи точки с координатой х на участке d x.
· Вероятность обнаружения частицы в интервале от х 1 до х 2
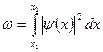 .
.
· Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика
1)  (собственная нормированная волновая функция);
(собственная нормированная волновая функция);
2) 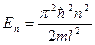 (собственное значение энергии),
(собственное значение энергии),
где n – квантовое число (n = 1,2,3…); l – ширина ящика.
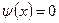 везде кроме 0 < x < l.
везде кроме 0 < x < l.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. Определите энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на второй.
Решение: Обобщенная формула Бальмера:
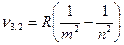
где ν – частота спектральных линий в спектре атома водорода, R – постоянная Ридберга, m – определяет серию (1,2,3,..), n – определяет отдельные линии соответствующей серии (n = m +1, m +2,..).

Рассчитаем: 
или 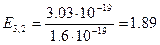 эВ.
эВ.
Пример 2. Определите длины волн, соответствующие: 1) границе серии Лаймана; 2) границе серии Бальмера; 3) границе серии Пашена. Проанализируйте результаты
Решение: 1) m = 1, n =2,3,.., 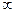 .
.

если 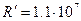 м-1,
м-1,  , при условии n =
, при условии n = 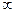
 м или 91 нм.
м или 91 нм.
2) m = 2, n = 3,4,.., 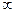 .
.
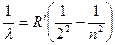 ,
,
если  , при условии n =
, при условии n = 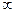
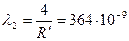 м или 364 нм.
м или 364 нм.
3) m = 3, n = 4,5,.., 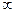 .
.
 ,
,
если  , при условии n =
, при условии n = 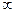
 м или 820 нм.
м или 820 нм.
Пример 3. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Найти длину волны λ де Бройля для двух случаев: 1) U 1= 51 В, 2) U 2 = 510 В.
Решение: Длина волны де Бройля:
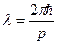 . (1)
. (1)
Запишем импульс для:
1. Нерелятивистского случая, когда Е к<< Е 0:
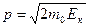 , (2)
, (2)
где Е к – кинетическая энергия электрона; Е 0 – энергия покоя электрона.
2. Релятивистского случая, когда Е к  Е0:
Е0:
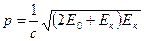 , (3)
, (3)
Тогда в соответствии с этим длина волны де Бройля будет:
1. Для нерелятивистского случая
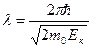 . (4)
. (4)
2. Для релятивистского случая
 . (5)
. (5)
Возникает вопрос: какую формулу использовать?
Сравним кинетические энергии электрона, прошедшего разность потенциалов U 1 = 51 В, U 2 = 510 В.
Кинетическая энергия электрона, прошедшего ускоренную разность потенциалов U: 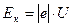 .
.
В соответствии с релятивизмом запишем:
Для нерелятивистского случая:  МэВ << Е 0, т.е. много меньше энергии покоя электрона:
МэВ << Е 0, т.е. много меньше энергии покоя электрона: 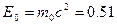 МэВ.
МэВ.
Следовательно, можно применить формулу длину волны для нерелятивистского случая:
 . (6)
. (6)
Известно:
 м – комптоновская длина волны.
м – комптоновская длина волны.
Тогда:
 м или 172 пм.
м или 172 пм.
Для релятивистского случая:
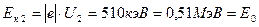 – применима релятивистская формула:
– применима релятивистская формула:
Е к2 = 0,51 МэВ = m0c2.
 пм.
пм.
Пример 4. На грань кристалла никеля падает параллельный пучок электронов. Кристалл поворачивают так, что угол скольжения θ изменяется. Когда этот угол становится равным 640, наблюдается максимальное отражение электронов, соответствующее дифракционному максимуму первого порядка. Принимая расстояние d между атомными плоскостями кристалла равным 200 пм, определите длину волны де Бройля λ электрона и их скорость.
Решение: К расчету дифракции электрона от кристаллической решетки применяется уравнение Вульфа – Брэгге, которое используется в случае рентгеновского излучения:
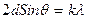 ,
,
где d – расстояние между атомными плоскостями кристалла, θ – угол скольжения, k – порядковый номер дифракционного максимума, λ – длина волны де Бройля.
Отсюда 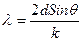 ,
,
находим  м или 360 пм.
м или 360 пм.
Из формулы длины волны де Бройля: 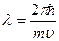 , найдем скорость:
, найдем скорость:
 м/с.
м/с.
Date: 2015-08-15; view: 568; Нарушение авторских прав