Геометрическая оптика. · Скорость света в среде

· Скорость света в среде

,

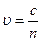где с – скорость света в вакууме; n – показатель преломления среды.

· Фокусное расстояние сферического зеркала

,

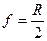где R – радиус кривизны зеркала.

· Оптическая сила сферического зеркала

.

Единица измерения оптической силы диоптрия (Дпт).

· Формула сферического зеркала

,

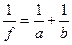где a и b - расстояния от полюса зеркала до предмета и изображения соответственно.

Если изображение предмета мнимое, то величина b берется со знаком минус.

Если фокус сферического зеркала мнимый (зеркала выпуклое), то величина f берется со знаком минус.

· Закон преломления света

,

где φ – угол падения; ψ – угол преломления; n ₂₁ – относительный коэффициент преломления или коэффициент преломления второй среды относительно первой (рис. 46).

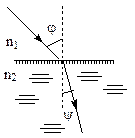
Рис. 46. Закон преломления света

· Оптическая сила тонкой линзы

,

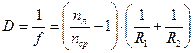где f – фокусное расстояние линзы; n _л – абсолютный показатель преломления вещества линзы; n _ср – абсолютный показатель преломления окружающей среды.

Радиусы R ₁ и R ₂ выпуклых поверхностей берутся со знаком плюс, вогнутых – со знаком минус.

Оптическая сила двух тонких сложенных вплотную линз

.

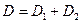· Формула тонкой линзы

,

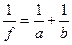где a – расстояние от оптического центра линзы до предмета; b – расстояние от оптического центра линзы до изображения.

Если фокус мнимый (линза рассеивающая, рис. 47), то величина f отрицательна.

Если изображение мнимое, то величина b отрицательна.

Рис. 47. Виды линз. Собирающие: 1 – двояковыпуклая, 2 – плоско-выпуклая,

3 – вогнуто-выпуклая; рассеивающие: 4 – двояковогнутая,

5 – плоско-вогнутая, 6 – выпукло-вогнутая

· Угловое увеличение лупы

,

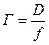где D – расстояние наилучшего зрения (D = 25 см).

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. На рисунке приведена схема перископа, который содержит два зеркала S ₁ и S ₂ , установленные под углом 45⁰ к трубе перископа (рис. 48). Лучи света от предмета AB через верхнее отверстие трубы перископа CD попадают на зеркало S ₁ , отражаются от него и, пройдя по трубе, попадают на зеркало S ₂ . Отразившись от зеркала S ₂, свет через нижнее отверстие трубы EF попадает в глаз наблюдателя (точка O). Определить наименьшую ширину h верхнего отверстия перископа, позволяющего наблюдать во весь рост человека высотой H, стоящего от перископа на расстоянии L, если расстояние между зеркалами по вертикали равно L₁ .

Решение: Выберем два крайних луча AC и BD, лежащие в плоскости чертежа. Поскольку плоскости зеркал перпендикулярны к плоскости чертежа, то после отражения лучи AC и BD также останутся в плоскости чертежа (рис. 49). Заметим, что после второго отражения луч возвращается к своему первоначальному направлению. Поэтому лучи AC и BD можно изобразить в виде прямых, сходящихся в точке O. Отрезок AB – высота H рассматриваемого человека, CD и EF – размеры соответственно верхнего и нижнего отверстий перископа.

В треугольнике OAB проведем высоту OM. Из подобия треугольников OAB и OСD следует, что (1)

Согласно условию задачи, AB = H, CD = h, KM = L. Так как расстоянием от нижнего отверстия до глаза можно пренебречь, то 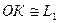OK L₁ . Тогда из соотношения (1) получим

,

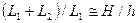откуда .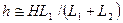

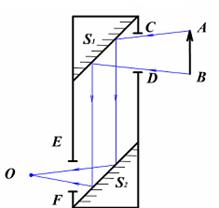Рис. 48. Схема перископа

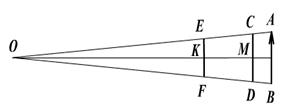Рис. 49. Ход лучей

Пример 2. Светящуюся точку, находящуюся в среде (рис. 50) с показателем преломления n ₁, рассматривают невооруженным глазом из среды с показателем преломления n ₂. Каково будет кажущееся расстояние точки от границы раздела сред, если точка находится от этой границы на расстоянии h ₁, а глаз расположен так, что в него попадают лучи, падающие на границу раздела под небольшими углами? Наблюдатель находится в оптически менее плотной среде (n ₁ > n ₂).

Решение: Выберем из пучка лучей, попадающих в глаз наблюдателя, два луча A 0 C и A 0 D. Первый луч падает перпендикулярно границе раздела сред и идет во вторую среду не преломляясь. Второй луч, переходя во вторую оптически менее плотную среду, отклоняется от своего начального направления. Лучи, вышедшие из точки A 0, кажутся наблюдателю выходящими из точки A 1, являющейся мнимым изображением точки A 0.

Рис. 50. Граница раздела двух сред

Пример 3. Радиус кривизны вогнутого зеркала R = 20 см. На рас­стоянии а ₁ = 30 см от зеркала поставлен предмет высотой y ₁ = 1см. Найти положение и высоту у ₂ изображения. Дать чер­теж.

Решение: Фокусное расстояние зеркала см. Подставим значения а 1 и F в формулу вогнутого зеркал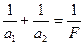а: ; отсюда см. Т. к. стержень расположен за центром зеркала (рис. 51), то его изображение действительное (f >0), обратное, уменьшенное.

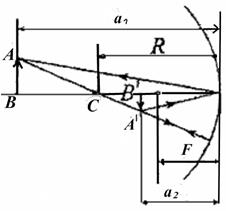Рис. 51. Построение предмета

Увеличение k = 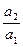= 0,5.

Следовательно, высота изображения y₂ = ky₁ = 0,5 см.

Date: 2015-08-15; view: 1452; Нарушение авторских прав