Законы теплового излучения и явление фотоэлектрического эффекта. · Закон Стефана-Больцмана

· Закон Стефана-Больцмана

,

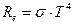где R _e – энергетическая светимость черного тела; T – термодинамическая температура; σ = 5,67∙10^-8 [Вт/(м²∙К⁴)]– постоянная Стефана-Больмана.

· Закон смещения Вина

,

где λ _max – длина волны, на которую приходится максимум энергии излучения; b = 2,90∙10^-3 [м∙К] – постоянная Вина.

· Формула Релея-Джинса

,

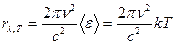где 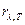– спектральная плотность энергетической светимости; 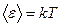–средняя энергия осциллятора с собственной частотой ν; с – скорость света в вакууме.

· Энергия фотона

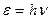или ,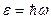

где h – постоянная Планка; 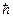– постоянная Планка, деленная на 2π; ν – частота фотона; ω – циклическая частота.

· Масса фотона

.

· Импульс фотона

.

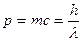· Формула Эйнштейна для фотоэффекта

,

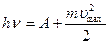где hν – энергия фотона, падающего на поверхность металлов; А – работа выхода электрона с поверхности металла; - максимальная кинетическая энергия фотоэлектрона.

· Красная граница фотоэффекта

, или ,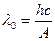

где ν ₀ – минимальная частота света, при которой еще возможен фотоэффект; λ ₀ – максимальная длина волны, при которой еще возможен фотоэффект.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. Температура внутренней поверхности муфельной печи при открытом отверстии площадью S = 30 см² равна Т = 1,3 кК. Принимая, что отверстие печи излучает как черное тело, определите, какая часть мощности рассеивается, если потребляемая печью мощность составляет Р = 1,5 кВт. (Постоянная Стефана-Больцмана σ = 5.67∙10^-8 Вт/м²∙К⁴).

Решение: Запишем формулы мощности излучения и рассеивания:

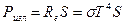и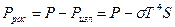

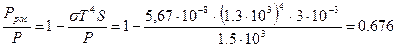
Пример 2. Принимая Солнце за черное тело и учитывая, что его максимальной спектральной плотности энергетической светимости соответствует длина волны 500 нм, определите: 1) температуру поверхности Солнца; 2) энергию, излучаемую Солнцем в виде электромагнитных волн за 10 мин; 3) массу, теряемую Солнцем за это время за счет излучения.

Решение: 1) Для нахождения максимальной длины волны Вин установил зависимость между 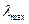и температурой Т – закон смещения Вина: 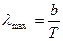, где b = 2,9·10^-3 м·К – постоянная Вина.

Отсюда выражаем температуру: 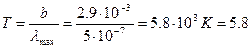кК

2) Согласно закону Стефана – Больцмана, энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической температуры: 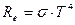, где R _е – энергетическая светимость; σ = 5,67·10^-8 Вт/(м²·К⁴) – постоянная Стефана-Больцмана.

Энергия, излучаемая Солнцем (по условию задачи АЧТ):

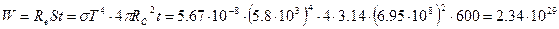Дж

3) Зная Е = mc², выразим массу, которая теряется за счет излучения:

кг.

Пример 3. Определите силу тока, протекающего по вольфрамовой проволоке диаметром d = 0,8 мм, температура которой в вакууме поддерживается постоянной и равной t = 2800 ⁰С. Поверхность проволоки считать серой с поглощательной способностью A_Т = 0,343. Удельное сопротивление проволоки при данной температуре 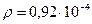Ом∙см. Температура окружающей проволоку среды t ₀ = 17 ⁰С.

Решение: Зная закон Ома, выразим мощность: Р = I ² R

Отсюда сила тока 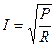(1)

Определение мощности: Р = Р_изл - Р_погл

Где мощность излучения: 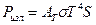и мощность поглощения:

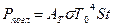, то Р = 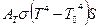(2)

Известно, площадь проволоки: S = πdl, радиус: .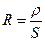

Площадь поперечного сечения проволоки:

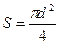. (3)

Подставляя (2) и (3) в (1), найдем:

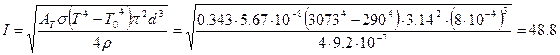А.

Пример 4. На плоский алюминиевый электрод падает ультрафиолетовое излучение с длиной волны λ = 90 нм. На какое максимальное расстояние d от его поверхности может удалиться фотоэлектрон, если вне электрода имеется однородное электрическое поле напряженностью E =8 В/см, задерживающее этот фотоэлектрон? Красная граница фотоэффекта для алюминия λ ₀ = 332 нм.

Решение: Из уравнения Эйнштейна для фотоэффекта:

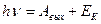(1)

Найти кинетическую энергию фотоэлектрона Е_К, которую он имеет сразу после вылета из электрода, и приравнять ее к работе однородного электрического поля: 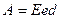(2)

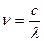задерживающего электрон. Отсюда можно найти искомое расстояние d. Из выражения (1): , где и .

С учетом , поскольку Е_К = А, то приравняв правые части равенств (2) и (3), получим: ,

откуда находим: .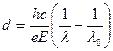

Вычисли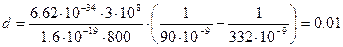м: м.

Date: 2015-08-15; view: 516; Нарушение авторских прав