Кейбір біртекті денелердің өстік инерция моменттері

Кейбір біртекті денелердің инерция моменттерін есептеуге мүмкіндік беретін өрнектерді алайық.

1. Біртекті жіңішке сырық. Ұзындығы , массасы М біртекті жіңішке сырықты қарастырайық. Сырық бойымен Ах өсін бағыттап, сырықтың ұшы арқылы оған перпендикуляр өтетін Az өсіне қатысты осы сырықтың инерция моментін санайық (3.27 сурет).

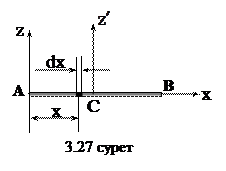Az өсінен h = x қашықтықта жататын ұзындығы сырық элементін бөлеміз. Az өсіне қатысты сырықтың инерция моменті үшін 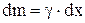, ал біртекті дене үшін 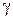- тұрақты шама болғандықтан (4.2.3) өрнегіне сәйкес:

.

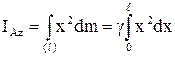Интегралдасақ, мынаны аламыз: .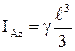

Біртекті сырық үшін 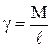екенін ескеріп, нәтижесінде біртекті сырықтың оның ұшы арқылы сырыққа перпендикуляр өтетін өске қатысты инерция моментінің өрнегін аламыз:

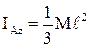(4.2.7)

(4.2.6) Гюйгенс-Штейнер теоремасын қолданып, біртекті жіңішке сырықтың оның массалар центрі арқылы сырыққа перпендикуляр өтетін 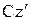өсіне қатысты инерция моментін алуға болады (3.27 сурет):

,

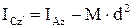мұндағы 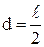– Oz пен 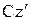өстері арасындағы қашықтық, ал (4.2.7) өрнегіне сәйкес 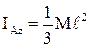, демек:

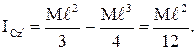
Сонымен, біртекті жіңішке сырықтың оның массалар центрі арқылы сырыққа перпендикуляр өтетін өске қатысты инерция моменті:

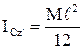. (4.2.8)

2. Біртекті жіңішке дөңгелек сақина. Радиусы R, массасы М біртекті сақинаны қарастырып, сақинаның массалар центрі арқылы оған перпендикуляр өтетін өсіне қатысты инерция моментін табайық (3.28 сурет). Сақинаның барлық нүктелері өсінен h = R қашықтықта жатқандықтан, (4.2.1) өрнегі бойынша:

.

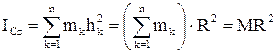Сонымен, біртекті жіңішке дөңгелек сақинаның оның центрі арқылы сақина жазықтығына перпендикуляр өтетін өске қатысты инерция моменті былай анықталады:

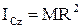. (4.2.9)

3. Біртекті дөңгелек диск. Радиусы R, массасы М біртекті жіңішке диск берілсін (3.29 сурет). Оның массалар центрі арқылы дискіге перпендикуляр өтетін өсіне қатысты инерция моментін санайық. Ол үшін дискіні жіңішке сақиналарға бөліп, олардың радиусы r және ені dr сақинаны қарастырамыз. Бұл сақинаның ауданы , демек оның массасы 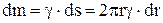. Сонда (4.2.3) өрнегі бойынша:

.

Сақинаның тығыздығы 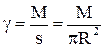екенін ескерсек, нәтижесінде біртекті жіңішке дискінің массалар центрі арқылы дискіге перпендикуляр өтетін өске қатысты инерция моменті саналатын өрнек аламыз:

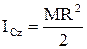. (4.2.10)

Радиусы R, массасы М біртекті цилиндрдің оның Oz симметрия өсіне қатысты инерция моменті де (4.2.10) өрнегімен саналады (3.30 сурет).

Date: 2015-08-15; view: 2071; Нарушение авторских прав