Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Вычисление определителей методом Гаусса
|
|
Итак, применим метод Гаусса для вычисления определителя ∆. При решении системы уравнений:
Ax = b
методом Гаусса мы путём преобразования по схеме единственного деления привели её к треугольному виду:
B x = β,
где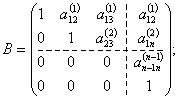 
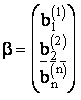
Определитель detB = 1.
Элементы матрицы B получились из матрицы A с помощью следующих элементарных преобразований:
1) деления на ведущие элементы a 11 матрицы A,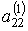 
матрицы 
,..., 
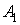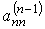матрицы An-1.
2) вычитания из строк матрицы A и промежуточных матриц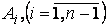 
чисел, пропорциональных элементам соответствующих ведущих строк.
При первой операции определитель матрицы также делится на соответствующий ведущий элемент, т.е.
.
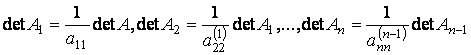Следовательно:
,
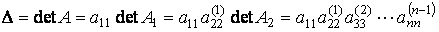т.е. определитель равен произведению ведущих элементов для соответствующей схемы Гаусса.
При второй операции определитель не изменится
.
2222222Требуется найти для исходной матрицы А обратную матрицу А-1
по методу исключения Гаусса.
Пример 1. Методом исключения Гаусса найдем матрицу, обратную к матрице
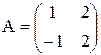
Решение:
К матрице А справа приписывается единичная матрица того же порядка (А|E)
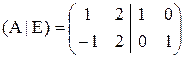
Матрица (А|E) приводится элементарными преобразованиями первого и второго типов к ступенчатому виду
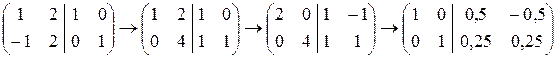
Последняя матрица имеет ступенчатый вид
3. Выписывается обратная матрица. Это матрица, стоящая справа в последней преобразованной матрице.
В последней матрице слева стоит единичная матрица E.
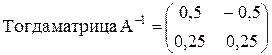
Пример 2.
Методом Гаусса найдем матрицу, обратную к матрице
.
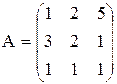Решение:
К матрице А справа приписывается единичная матрица того же порядка (А|E)
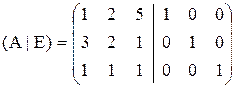
Матрица (А|E) приводится элементарными преобразованиями первого и второго типов к ступенчатому виду
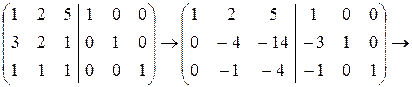
поменяем местами вторую и третью строки
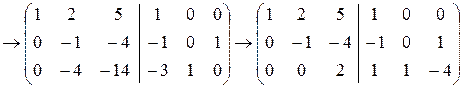
Последняя матрица имеет ступенчатый вид.
3. Полученная ступенчатая матрица элементарными преобразованиями 1-го, 2-го и 3-го типов приводится к виду, где слева будет матрица Е. Преобразования начинаются с последней строки.
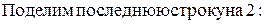
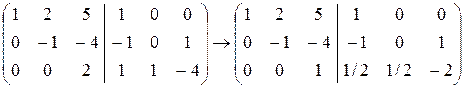
К элементам второй строки прибавим элементы третьей, умноженные на 4, а к элементам первой строки прибавим элементы третьей, умноженные на 5:
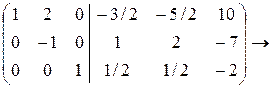
Все элементы второй строки умножим на (-1)
Из элементов первой строки вычитаем элементы второй, умноженные на 2
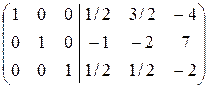
4. Выписывается обратная матрица. Это матрица, стоящая справа в последней преобразованной матрице.
В последней матрице слева стоит единичная матрица E.
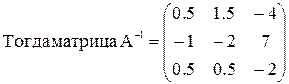
Date: 2015-07-25; view: 678; Нарушение авторских прав