Потенциальная помехоустойчивость когерентного приема двоичных и многопозиционных сигналов

Определим потенциальную помехоустойчивость для двоичной системы с аддитивным БГШ в канале, когда при приёме точно известны оба ожидаемых сигнала: s ₁(t)и s ₀(t), полагая, что априорные вероятности этих сигналов одинаковы. Приходящий сигнал z (t)является случайным, так как, во-первых, заранее не известна реализация передаваемого сигнала, во-вторых, он содержит случайную помеху N (t).

В этом случае согласно (5.26) алгоритм оптимального приема

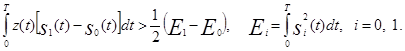(5.44)

При выполнении неравенства (5.44) оптимальный приёмник регистрирует символ 1, соответствующий сигналу s ₁(t), в противном случае - символ 0, соответствующий сигналу s ₀(t). Если действительно передаётся символ 1, то z (t)= s ₁(t) +N (t). При этом вероятность ошибки определяется вероятностью того, что неравенство (5,44) не выполнено, т.е. вероятностью выполнения обратного неравенства

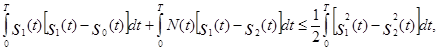
которое легко привести к следующему виду:

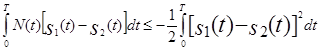. (5.45)

Аналогичное соотношение получается, если предположить, что передаётся символ 0. Следовательно, в обоих случаях вероятности ошибки p (0|1)= p (l|0)= p и сформированный модемом двоичный дискретный канал симметричен.

Запишем (5.45) в виде

x< -0,5 E_э, (5.46)

где 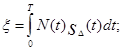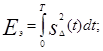s _D(t)= s ₁(t)- s ₂(t).

Если N (t) — нормальный стационарный белый шум с нулевым средним и односторонней спектральной плотностью мощности N ₀, то x - нормально распределённая величина (так как она определяется линейной операцией над нормальным же случайным процессом). Её математическое ожидание 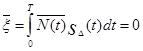, а дисперсия

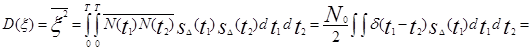
(5.46a)

Поэтому вероятность выполнения неравенства (5.46), т.е. вероятность ошибки,

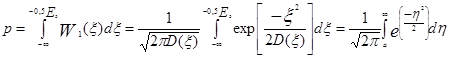(5.47)

где произведена замена переменной 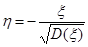и введено обозначение

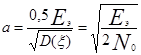. (5.48)

Функция 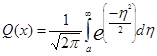табулирована и называется дополнительной функцией ошибок[1]⁾. Через Q -функцию можно (5.47) записать в виде

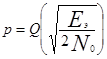(5.49)

При заданной интенсивности помехи N ₀потенциальная помехоустойчивость двоичной системы зависит только от так называемой эквивалентной
энергии сигналов

(5.50)

которая равна квадрату расстояния между сигнальными точками в пространстве Гильберта.

Вывод.

Таким образом, помехоустойчивость выше (вероятность ошибки меньше) у той системы, у которой больше эквивалентная энергия используемых сигналов, независимо от формы используемых сигналов. Последние, в частности, могут быть как простыми (отрезками синусоиды с малой базой), так и сложными (шумоподобными, с большой базой).

Date: 2015-07-25; view: 775; Нарушение авторских прав