
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Главные напряжения и главные площадки
|
|
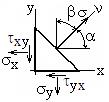 Найти главные напряжения и положения главных площадок.
Найти главные напряжения и положения главных площадок.
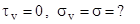 tg
tg 
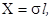
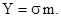 (2)
(2)
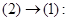
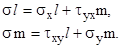
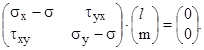 (3)
(3)
Однородная система алгебраических уравнений. Тривиальное (нулевое) решение системы (3)
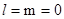
не годится, так как направляющие косинусы должны удовлетворять условию
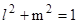 (4)
(4)
Чтобы система (3) имела нетривиальное решение, определитель матрицы должен быть равным нулю, т.е.
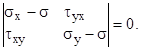 (5)
(5)
(3), (4) решаются совместно. (5) представляет квадратное уравнение
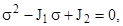 (6)
(6)
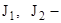 инварианты напряжённого состояния.
инварианты напряжённого состояния.
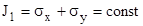 - сумма нормальных напряжений.
- сумма нормальных напряжений.
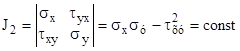 -определитель матрицы напряжений. Решаем квадратное уравнение (6). Два корня, два главных напряжения
-определитель матрицы напряжений. Решаем квадратное уравнение (6). Два корня, два главных напряжения
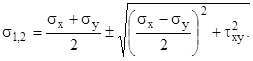 (7)
(7)
Третье главное напряжение действует перпендикулярно чертежу, на основании призмы. Эта площадка свободна от нагрузки, поэтому
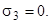
Полученные напряжения должны быть переобозначены ввиду выше принятой нумерации главных напряжений
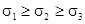 .
.
Положения главных площадок могут быть найдены из уравнений (3). Будем определять две площадки через тангенсы соответствующих углов наклона. Разделим их на 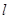 и легко найдём формулы для двух главных площадок
и легко найдём формулы для двух главных площадок
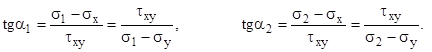 (8)
(8)
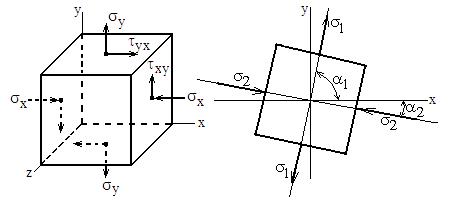
Пример. Имеется плоское напряжённое состояние, изображённое на рисунке.
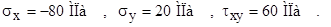
Найти главные напряжения и положения главных площадок.
-------------------------------------------------------------------------------
Счёт по формулам (7), (8) дал следующие релуьтаты:
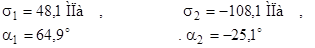
По значениям углов видно, что главные площадки взаимно перпендикулярны. 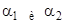 , определённые разными вариантами формул (8), точно совпадают.
, определённые разными вариантами формул (8), точно совпадают.
В заключение обратим внимание на то, что определение главных напряжений и положений главных площадок здесь полностью совпадает с проблемой определения собственных значений и собственных векторов квадратной матрицы в линейной алгебре.
4.Круговая диаграмма напряжённого состояния
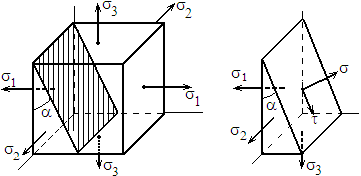
Используем формулы растяжения–сжатия в 2-х направлениях: 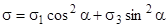 (1)
(1) 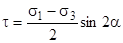 (2)
(2)

Формуле (1) легко придать вид
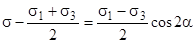 (3)
(3)
(2) и (3) возводим в квадрат и складываем
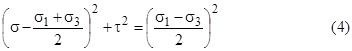
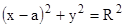 . (5)
. (5)
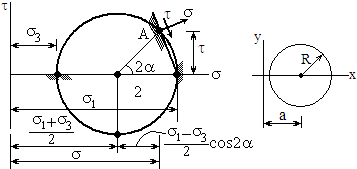 |
Это уравнение окружности в системе
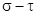 .
.
Центр окружности имеет координату  , радиус
, радиус 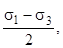 диаметр
диаметр 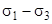 .Точка А имеет координаты
.Точка А имеет координаты 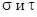 . Это круг Мора, круговая диаграмма напряжённого состояния. Можно построить три круга Мора. Из рисунка можно получить значение наибольшего касательного наряжения
. Это круг Мора, круговая диаграмма напряжённого состояния. Можно построить три круга Мора. Из рисунка можно получить значение наибольшего касательного наряжения
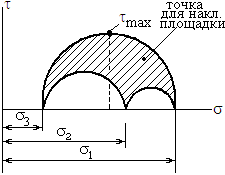
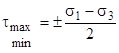 .
.
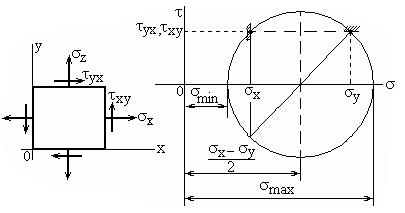
Для произвольного плоского напр. состояния.
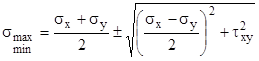
Круги Мора для различных случаев.
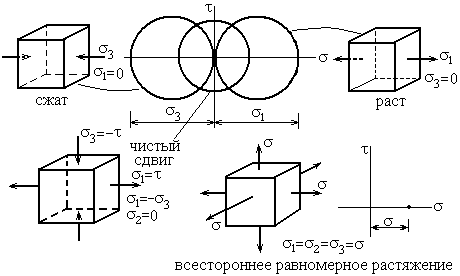
5.Основы теорий прочности
Оценка прочности конструкций является основной задачей технической механики. Механ. состояния: упругое, пластическое и разрушения.
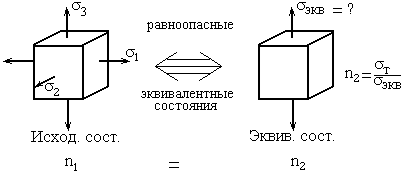
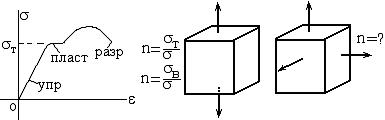
Коэф. зап.?= число, показыв. во сколько раз следует увеличить все уi чтобы изменить мех. состояние.
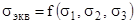 - как найти эту функцию?
- как найти эту функцию?
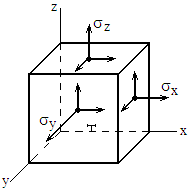 Существует несколько теорий прочности позволяющих найти эту функцию, а, следовательно, и вычислить
Существует несколько теорий прочности позволяющих найти эту функцию, а, следовательно, и вычислить 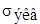 . Тогда, прочность конструкции определяется как для растянутого стержня, т.е. проверяется условие прочности
. Тогда, прочность конструкции определяется как для растянутого стержня, т.е. проверяется условие прочности
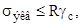
где R –расчётное сопротивление материала, 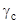 - коэффициент условий работы.
- коэффициент условий работы.
Теории прочности понадобятся при изучении более сложных видов деформаций будут изучены позже.
Date: 2015-07-25; view: 2605; Нарушение авторских прав