Необходимые и достаточные условия

В следующих предложениях вместо многоточия поставьте слова «необходимо, но недостаточно» или «достаточно, но не необходимо», а где возможно «необходимо и достаточно» так, чтобы получилось истинное утверждение:

Задача 1. Пусть на отрезке [a, b] определена непрерывная функция f(x) имеющая на промежутке [a, b] конечные производные, тогда:

Для того, чтобы функция f(x) была постоянной на отрезке [a, b] необходимо и достаточно, чтобы 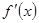=0 для .

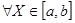Решение:

F(x)=const на [a, b] 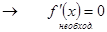- истина

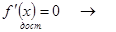F(x)=const на [a, b] – истина

Задача 2. Для того, чтобы два вектора 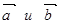в пространстве были перпендикулярными, необходимо и достаточно, чтобы их скалярное произведение равнялось нулю

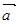┴ - истина

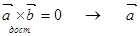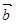┴ - истина

Задача 3. Для того, чтобы уравнение 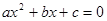имело действительные корни, необходимо и достаточно, чтобы .

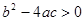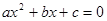имело действительные корни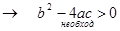

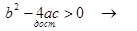
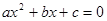имело действительные корни

Задача 4. Для того, чтобы в точке x₀ функция f(x) имела экстремум, необходимо, чтобы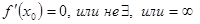

Решение:

функция f(x) в точке x₀ имеет экстремум 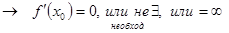- истина

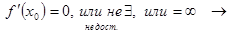функция f(x) в точке x₀ имеет экстремум – ложь

контрпример: .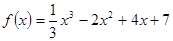

Задача 5.Для того, чтобы четырехугольник был квадратом, необходимо, но не достаточно, чтобы его диагонали были перпендикулярны.

Решение:

ABCD – квадрат 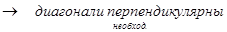- истина

ABCD – квадрат – ложь

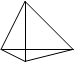B

контрпример: A C

D

Задача 6. Для того, чтобы уравнение cos x = a имело решение, необходимо, но не достаточно, чтобы .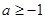

Решение:

Cos x = a - имеет решение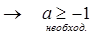

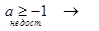Cos x = a - имеет решение – ложь

контрпример: a = 3.

Задача 7. Для того, чтобы в точке x₀ функция f(x) имела разрыв второго рода, достаточно, чтобы = ∞.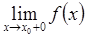

Решение:

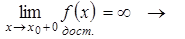функция f(x) в точке x₀ имеет разрыв второго рода – истина.

Задача 8. Для того, чтобы выражение x² – 2x – 3 равнялось нулю, достаточно, но не необходимо, чтобы x = -1.

Решение:

x² – 2x – 3 = 0 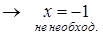- ложь

контрпример: x = 3.

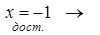x² – 2x – 3 = 0 – истина

Date: 2015-07-25; view: 1825; Нарушение авторских прав