
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Равносильные формулы алгебры высказываний
|
|
Две формулы алгебры высказываний А и В называются равносильными или эквивалентными, если они принимают одинаковые логические значения на любом наборе значений входящих в формулы элементарных высказываний.
Равносильность формул будем обозначать знаком 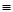 , а запись А
, а запись А 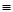 В означает, что формулы А и В равносильны.
В означает, что формулы А и В равносильны.
Например, равносильны формулы:
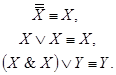
Формула А называется тождественно истинной (или тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных.
Например, тожественно истинны формулы 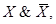
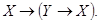
Формула А называется тождественно ложной (или противоречием), если она принимает значение 0 при всех значениях входящих в нее высказываний.
Например, тождественно ложна формула 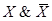 .
.
Формула А называется выполнимой, если она принимает значение 1 при всех значениях входящих в нее высказываний.
Например, выполнима формула 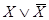 .
.
Ясно, что отношение равносильности рефлексивно, симметрично и транзитивно.
Между понятиями равносильности и операцией 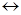 существует следующая связь: если формулы А и В равносильны, то формула А
существует следующая связь: если формулы А и В равносильны, то формула А 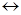 В - тавтология, и обратно, если формула А
В - тавтология, и обратно, если формула А 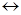 В - тавтология, то формулы А и В равносильны.
В - тавтология, то формулы А и В равносильны.
Важнейшие равносильности алгебры высказываний можно разбить на следующие группы.
1.Равносильности алгебры Буля:
1.Закон двойного отрицания:
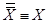
2. Коммутативность:
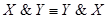

3. Ассоциативность:
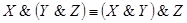
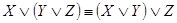
4. Дистрибутивность & относительно 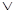 :
:
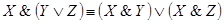
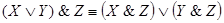
5. Дистрибутивность  относительно &:
относительно &:
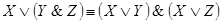
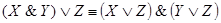
6. Законы де Моргана:
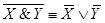
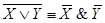
7. Законы поглашения:
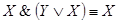

8. Законы идемпотентности:
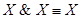
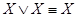
9. Свойства констант:
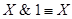
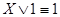
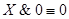
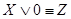
10. Закон противоречия:
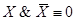
11. Закон исключения третьего:
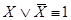
2. Равносильности, выражающие одни логические операции через другие:
12. 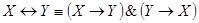
13. 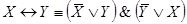
14. 
15. 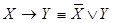
16. 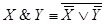
17. 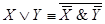
Date: 2015-07-25; view: 1383; Нарушение авторских прав