Пример выполнения задания. Даны результаты равноточных независимых многократных измерений одного и того же угла

Даны результаты равноточных независимых многократных измерений одного и того же угла. Определить: 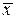, m, M, , .

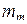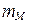Построить доверительный интервал, с вероятностью 0,90 накрывающий истинное значение угла. Составим таблицу.

Таблица 2.1
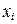
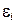
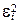
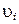
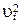
№ П.п.	Результаты измерений					примечания
	67°33′44″	+4		–0,7	0,49	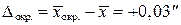Контроли: а) 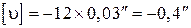; б) .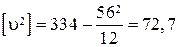
	40″	+0		–4,7	22,1
	43″	+3		–1,7	2,89
	45″	+5		+0.3	0,09
	46″	+6		+1,3	1,69
	43″	+3		–1,7	2,89
	48″	+8		+3,3	10,9
	45″	+5		+0,3	0,09
	48″	+8		+3,3	10,9
	46″	+6		+1,3	1,69
	47″	+7		+2,3	5,29
	41″	+1		–3,7	13,7
S		+56		–0,4	72,72

1. Вычисление среднего арифметического

.

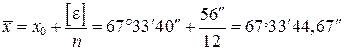В качестве наиболее надёжного значения принимаем среднее арифметическое, округлённое до десятых долей секунды

.

2. Вычисление уклонений , а также сумм 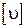, , 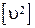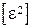непосредственно в таблице 3.1 и по контрольным формулам:

a) , b) .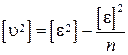

(2.5)

Расхождение между суммой 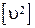, которую получили непосредственно в таблице, и её контрольным значением допускается в пределах (2–3)% от величины 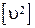. Как видно из результатов вычислений (см. примечания в таблице 2.1), контроли выполнены.

3. Вычисление средней квадратической ошибки отдельного результата измерений по формуле Бесселя:

.

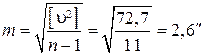4. Вычисление средней квадратической ошибки наиболее надёжного значения измеряемого угла:

.

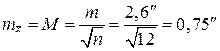5. Оценим точность полученных значений m и M по формулам:

, .

(2.6)

6. Построим доверительный интервал для истинного значения измеряемого угла. Для вероятности и числа степеней свободы 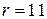(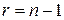) по таблице Стьюдента находим коэффициент , а затем по формуле (2.4) вычисляем границы интервала:

,

,

.

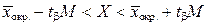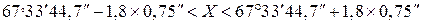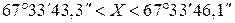Ответ: интервал 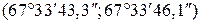с доверительной вероятностью 0,90 накрывает истинное значение угла. В сокращённой форме ответ имеет вид:

.

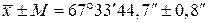Date: 2015-07-24; view: 1578; Нарушение авторских прав