
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример выполнения задания
|
|
Для решения этой первой задачи теории ошибок используем методику, изложенную в разделе математической статистики, а также выполним вычисления по формулам (1.1–1.5) настоящего раздела.
В таблице 1.1 даны невязки 32‑х треугольников. Невязки 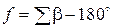 можно считать истинными ошибками D, так как сумму углов в треугольнике можно рассматривать как измеренную величину, истинное значение которой равно
можно считать истинными ошибками D, так как сумму углов в треугольнике можно рассматривать как измеренную величину, истинное значение которой равно 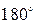 . Выполнить исследование ряда невязок
. Выполнить исследование ряда невязок 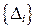 на нормальный закон распределения.
на нормальный закон распределения.
| Таблица 1.1 | |||||||
| № | невязки D i | № | невязки D i | № | невязки D i | № | невязки D i |
| –0,76″ | +1,29″ | +0,71″ | +0,22″ | ||||
| +1,52″ | +0,38″ | +1,04″ | +0,06″ | ||||
| –0,24″ | –1,03″ | –0,38″ | +0,43″ | ||||
| +1,31″ | +0,00″ | +1,16″ | –1,28″ | ||||
| –1,27″ | –1,23″ | –0,19″ | –0,41″ | ||||
| –1,88″ | –1,38″ | +2,28″ | –2,50″ | ||||
| +0,01″ | –0,25″ | +0,07″ | +1,92″ | ||||
| –0,69″ | –0,73″ | –0,95″ | –0,62″ |
Найдём ряд сумм, необходимых для дальнейшего исследования:
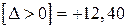 ;
; 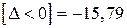 ;
; 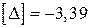 ;
; 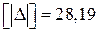 ;
;
 ;
; 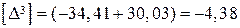 ;
; 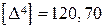 .
.
Решение:
1. Вычисление оценок параметров нормального распределения 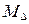 ,
, 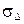 , кривая плотности которого определяется выражением:
, кривая плотности которого определяется выражением:
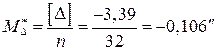 ,*)
,*)
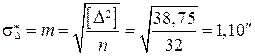 .
.
2. Вычисление средней ошибки 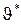 и коэффициента
и коэффициента  :
:
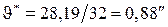 ;
;
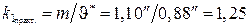 ;
; 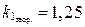 .
.
3. Определение вероятной ошибки 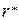 и коэффициента
и коэффициента 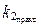 .
.
Располагаем истинные ошибки в ряд по возрастанию их абсолютных величин:
+0,00; +0,01; +0,06;+0,07; –0,19; +0,22; –0,24; –0,25; +0,38; –0,38; –0,41; +0,43; –0,62; –0,69; +0,71; –0,73; –0,76; –0,95; –1,03; +1,04; +1,16; –1,23; –1,27; –1,28; +1,29; +1,31; –1,38; +1,52; –1,88; +1,92; +2,28; –2,50.
Находим:
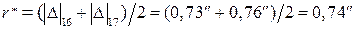 ;
;
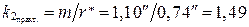 ;
; 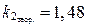 .
.
4. Построение статистического группированного ряда.
Распределим невязки (табл. 1.2) в двенадцати интервалах (длину интервала примем равной половине средней квадратической ошибки, т.е. 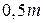 ).
).
| Таблица 1.2 | |||||||
| № п/п | длины интервалов в долях m | длины
интервалов
в секундах
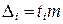
| число ошибок mi | частоты 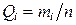
| высоты
прямо-угольников
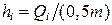
| ||
| –3,0 m | –2,5 m | –3,30″ | –2,75″ | 0,000 | 0,000 | ||
| –2,5 m | –2,0 m | –2,75 | –2,20 | 0,031 | 0,056 | ||
| –2,0 m | –1,5 m | –2,20 | –1,65 | 0,031 | 0,056 | ||
| –1,5 m | –1,0 m | –1,65 | –1,10 | 0,125 | 0,227 | ||
| –1,0 m | –0,5 m | –1,10 | –0,55 | 0,188 | 0,342 | ||
| –0,5 m | +0 | –0,55 | –0 | 0,156 | 0,284 | ||
| +0 | +0,5 m | –0 | +0,55 | 0,219 | 0,398 | ||
| +0,5 m | +1,0 m | +0,55 | +1,10 | 0,062 | 0,113 | ||
| +1,0 m | +1,5 m | +1,10 | +1,65 | 0,125 | 0,227 | ||
| +1,5 m | +2,0 m | +1,65 | +2,20 | 0,031 | 0,056 | ||
| +2,0 m | +2,5 m | +2,20 | +2,75 | 0,031 | 0,056 | ||
| +2,5 m | +3,0 m | +2,75 | +3,30 | 0,000 | 0,000 | ||
| ∑ | 1,000 | ― | |||||
| mi — число ошибок, попавших в i ‑й интервал, подсчитывается непосредственно. Если значение ошибки совпадает с границей интервала, то эту ошибку следует поместить в тот интервал, в котором теоретически ожидается большее число ошибок (см. рис 1.1) |
5. Построение гистограммы и выравнивающей её кривой распределения.
По данным таблицы 1.2 (столбцы 2 и 6) строим гистограмму (рис. 1.1) — график эмпирического распределения (на выбор масштаба изображения наложим лишь условие наглядности).
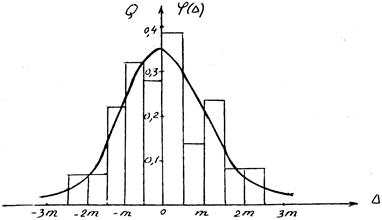
Рис. 1.1 — Гистограмма и выравнивающая кривая 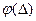
Вид гистограммы позволяет действительно предположить нормальный закон распределения ошибок D i. Теоретическая кривая, наилучшим образом выравнивающая (сглаживающая) гистограмму, определяется уравнением
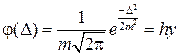 , ,
| (1.6) |
где 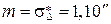 ;
; 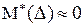 ;
; 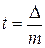 ;
; 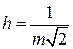 ;
; 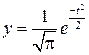 .
.
Вычисление ординат кривой 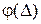 выполняем, используя таблицу Приложения A. Результаты вычислений поместим в таблице 1.3.
выполняем, используя таблицу Приложения A. Результаты вычислений поместим в таблице 1.3.
| Таблица 1.3 | |||||
| № п/п | левые границы интервалов D i | 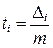
| yi | 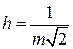
| 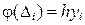
|
| 0,564 | 0,645 | 0,364 | |||
| 0,5m | 0,5 | 0,498 | ―"― | 0,321 | |
| 1,0m | 1,0 | 0,342 | ―"― | 0,220 | |
| 1,5m | 1,5 | 0,183 | ―"― | 0,118 | |
| 2,0m | 2,0 | 0,076 | ―"― | 0,049 | |
| 2,5m | 2,5 | 0,025 | ―"― | 0,016 | |
| 3,0m | 3,0 | 0,006 | ―"― | 0,004 |
По данным таблицы 1.3 (столбцы 2 и 6) на графике рис. 1.1 наносим ряд точек 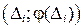 , которые соединяем плавной кривой. Левую ветвь кривой строим по тем же ординатам.
, которые соединяем плавной кривой. Левую ветвь кривой строим по тем же ординатам.
Как видно из графика, кривая j(D) удовлетворительно сглаживает гистограмму.
6. Применение критерия c2 ‑Пирсона.
Для оценки степени приближения статистического распределения (гистограммы) к теоретическому нормальному закону (кривой распределения) вычисляем величину
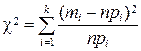 , ,
| (1.7) |
где
 . .
| (1.8) |
Результаты вычислений поместим в таблице 1.4.
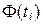 находят по таблице Приложения B для левых границ интервалов ti.
находят по таблице Приложения B для левых границ интервалов ti.
| Таблица 1.4 | |||||||
| № | Интервалы ti | 
| pi | mi | npi | 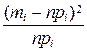
| |
| –3,0 | –2,5 | –0,5 | 0,0062 | 0,20 | 0,20 | ||
| –2,5 | –2,0 | –0,4938 | 0,0166 | 0,53 | 0,42 | ||
| –2,0 | –1,5 | –0,4772 | 0,0440 | 1,41 | 0,12 | ||
| –1,5 | –1,0 | –0,4332 | 0,0918 | 2,94 | 0,38 | ||
| –1,0 | –0,5 | –0,3414 | 0,1500 | 4,80 | 0,30 | ||
| –0,5 | +0 | –0,1914 | 0,1914 | 6,12 | 0,20 | ||
| +0 | +0,5 | +0 | 0,1914 | 6,12 | 0,13 | ||
| +0,5 | +1,0 | +0,1914 | 0,1500 | 4,80 | 1,63 | ||
| +1,0 | +1,5 | +0,3414 | 0,0918 | 2,94 | 0,38 | ||
| +1,5 | +2,0 | +0,4332 | 0,0440 | 1,41 | 0,12 | ||
| +2,0 | +2,5 | +0,4772 | 0,0166 | 0,53 | 0,42 | ||
| +2,5 | +3,0 | +0,4938 | 0,0062 | 0,20 | 0,20 | ||
| +3,0 | +∞ | +0,5 | ― | ― | ― | ― | |
| S | 1,0000 | 32,00 | 4,50 |
Число степеней свободы определяется формулой 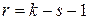 . Находим
. Находим 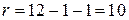 (k — число интервалов,
(k — число интервалов, 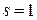 , так как только один параметр
, так как только один параметр 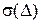 оценивался по выборке, а
оценивался по выборке, а  принято равным нулю).
принято равным нулю).
По таблице Приложения E по числу степеней свободы 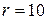 для
для 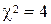 находим вероятность
находим вероятность 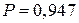 , а для
, а для 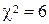 находим
находим 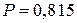 . Интерполируя, для
. Интерполируя, для 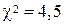 получим
получим 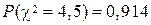 .
.
7. Вычисление оценок скошенности 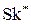 и эксцесса
и эксцесса 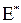 и проверка соотношений:
и проверка соотношений:
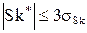 ; ; 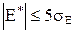 , ,
| (1.9) |
которые являются критериями нормального закона.
Находим:
1)  ;
;
2) 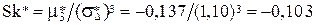 ;
;
3) 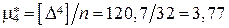 ;
;
4) 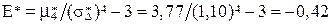 ;
;
5) 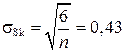 ;
; 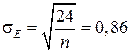
Как видно из вычислений, соотношения (1.9) выполняются.
В результате исследования приходим к выводу о том, что рассматриваемый ряд истинных ошибок является действительно рядом случайных ошибок, подчиняющихся приближенно нормальному закону, так как:
1) выполняются свойства случайных ошибок:
а) среднее арифметическое 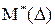 практически равно нулю,
практически равно нулю,
б) положительные и отрицательные ошибки, равные по абсолютной величине (см. гистограмму), примерно одинаково часто встречаются в данном ряде,
в) малые по абсолютной величине ошибки встречаются чаще, чем большие,
г) случайные ошибки D с заданной вероятностью b не превосходят определенного предела, равного 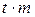 , ни одна из ошибок ряда не превышает предельной ошибки, равной
, ни одна из ошибок ряда не превышает предельной ошибки, равной
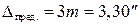 ;
;
2) коэффициенты 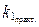 и
и 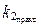 совпадают с их теоретическими значениями (
совпадают с их теоретическими значениями (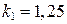 ;
; 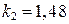 );
);
3) вероятность 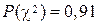 велика, так как значительно больше критического уровня значимости, равного 0,1;
велика, так как значительно больше критического уровня значимости, равного 0,1;
4) величины скошенности и эксцесса незначительно отличаются от нуля.
Date: 2015-07-24; view: 946; Нарушение авторских прав