Блок 18. Методы регрессионно-корреляционного анализа связи показателей

Корреляционные связи присутствуют в большинстве социально-экономических явлений. Установлению их наличия и определению тесноты связи между отдельными факторами помогает регрессионно-корреляционный анализ. Суть этого анализа заключается в построении и анализе экономико-математической модели уравнения регрессии, которая бы наиболее полно отражала зависимость признака от определяющих его факторов. Регрессионный анализ позволяет построить модель уравнения регрессии, корреляционный анализ дает оценку тесноты связи.

Проведение этого анализа предполагает прохождение ряда этапов:

- предварительный анализ;

- сбор информации и первичная ее обработка;

- построение модели;

- оценка и анализ модели.

Построение модели связано с выбором формы связи на основе собранных эмпирических данных. При выборе типа функции руководствуются расположением точек на корреляционном поле, а также содержанием исследуемой связи. Чаще всего используется линейное уравнение парной регрессии: ,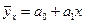

где х – факторный признак;

а₀ и а₁ – параметры уравнения.

Экономический смысл параметра а₀ – характеризует значение результативного признака независимо от роста факторного, а₁ – коэффициент регрессии, показывает, насколько изменится величина функции у при изменении факторного признака х.

Параметры определяются из системы двух уравнений для парной линейной регрессии, полученных на основе выравнивания по способу наименьших квадратов:

.

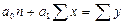
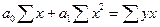Эту систему уравнений решаем способом определителей и находим параметры:

;

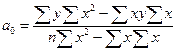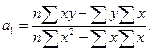
Если необходимо выразить нелинейность зависимости у от х, то могут быть использованы следующие уравнения регрессии:

,

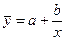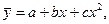
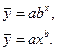
Решение математических уравнений связи предполагает вычисление по исходным данным их параметров. Применяется метод наименьших квадратов, где основное требование – минимальность сумм квадратов отклонений эмпирических данных y_i от выравненных

.

Для оценки тесноты связи применяются показатели вариации:

1. Общая дисперсия результативного признака - отражает совокупное влияние факторов:

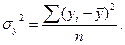
2. Факторная дисперсия результативного признака 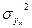- отражает вариацию только от воздействия изучаемого фактора х:

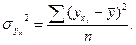
Характеризует колеблемость выравненных значений у_х от общей средней величины .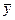

3. Остаточная дисперсия отображает вариацию результативного признака у от всех прочих, кроме х факторов:

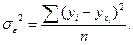
Соотношение между факторной 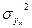и общей отражает меру тесноты связи между х и у.

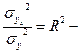индекс детерминации – доля факторной дисперсии в общей дисперсии. Если это выражение представить как 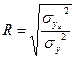, то R это будет индекс корреляции.

На основе правила сложения дисперсий ( = 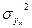+ 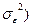индекс корреляции можно представить как: 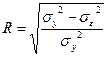или 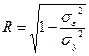. Индекс корреляции применяется для оценки тесноты связи при всех формах связи.

Для измерения тесноты линейной связи применяется линейный коэффициент корреляции:

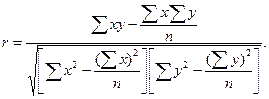
Качественная оценка тесноты связи показателей дается с помощью шкалы Чеддока:

Показатели тесноты связи	0,1-0,3	0,3-0,5	0,5-0,7	0,7-0,9	0,9-0,99
Характеристика силы связи	слабая	умеренная	заметная	высокая	весьма высокая

Рассмотрим на условном примере применение регрессионно-корреляционного анализа связи парной корреляции. Имеется выборочная информация о работе 8 гостиниц, у которых различная среднегодовая наполняемость гостиничных номеров и различная рентабельность их деятельности. В результате регрессионно-корреляционного анализа необходимо определить, существует ли прямая зависимость между наполняемостью гостиничных номеров и если она есть, то насколько она тесная:

N пп	Наполняе-мость (в %%) х	Рентабель- ность (в %%) у	х2	у2	ху	Выравненное (теоретическое) ух
		8,2 7,0 9,3 8,1 9,5 10,5 7,5 6,3		67,24 49,00 86,49 65,61 90,25 110,25 56,25 39,69	492,0 364,0 669,6 526,5 712,5 840,0 420,0 315,0	7,61 6,65 9,05 8,21 9,41 10,01 7,13 6,41
		66,4		564,78	4339,6	64,48

Определим параметры уравнения линейной парной регрессии :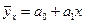

.

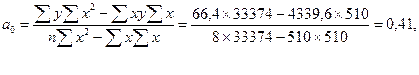
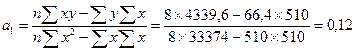Наше уравнение парной регрессии будет иметь вид: 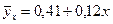. Подставим в это уравнение эмпирические значения х и рассчитаем теоретические значения 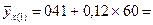7,61 и т. д.

Теперь определим тесноту связи между наполняемостью гостиниц и рентабельностью их деятельности:

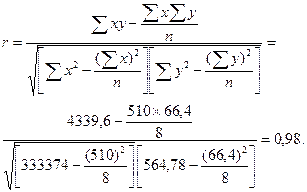
В результате проведенного анализа установлено, что между наполняемостью гостиниц и рентабельностью их деятельности существует прямая весьма высокая зависимость.

Date: 2015-07-24; view: 439; Нарушение авторских прав