
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Блок 17. Виды связей явлений
|
|
Все явления объективного мира находятся в причинно-следственных связях и взаимно обусловлены. Познание социально-экономических явлений означает познание их во всех или определяющих связях и взаимозависимостях. Одной из основных задач статистики является установление причинно-следственных связей, действующих в общественных явлениях. Особенность связей в социально-экономических явлениях состоит в том, что их закономерный характер проявляется лишь в массе явлений.
Известно, что 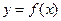 , т.е. результативный признак у является функцией от признака-фактора х и для того, чтобы воздействовать на у надо изменить х. Связи между признаками явлений и самими явлениями могут быть функциональными и корреляционными.
, т.е. результативный признак у является функцией от признака-фактора х и для того, чтобы воздействовать на у надо изменить х. Связи между признаками явлений и самими явлениями могут быть функциональными и корреляционными.
Функциональные – это такие связи, в которых каждому значению одного признака х на единицу соответствует изменение другого признака у на строго определенную величину. Например, увеличение радиуса окружности на 1 см. приводит всегда к увеличению длины окружности на 6,28 см., т. к. она определяется по формуле 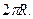
Корреляционные – это такие связи, когда при одном и том же значении признака х имеют место различные значения признака у, при этом между ними существует соотношение, когда определенному изменению признака х соответствуют среднее изменение признака у.
По направлению принято различать две формы связи: прямую и обратную. Прямая связь, при которой с ростом признака-фактора, возрастают значения результативного признака. В том случае, когда с увеличением признака-фактора, значения результативного уменьшаются имеет место обратная связь.
По форме выражения различают прямолинейные и криволинейные связи. Прямолинейной называется связь, которая может быть выражена уравнением прямой. Связь, которая может быть выражена уравнением какой-либо кривой линией, называется криволинейной.
В ходе статистического анализа возникает необходимость определения степени тесноты связи результативного фактора от вариации признака-фактора. Зная тесноту связи между отдельными факторами можно отобрать среди прочих наиболее важные и существенные факторыи осечь те, которые несущественно влияют на результативный признак фактор.
Для оценки тесноты связи между факторами существуют различные показатели. Простейшим из них является коэффициент корреляции знаков – коэффициент Г. Фетнера. 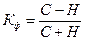 Расчет этого показателя осуществляется вычислением средних значений обоих признаков, а затем определяются знаки отклонения от средней для всех значений взаимосвязанных признаков. С- число совпадений знаков отклонений индивидуальных значений от средней, а Н – число несовпадений знаков. Коэффициент принимает значения от -1 до +1.Если коэффициент имеет знак плюс, то имеется прямая зависимость, если минус, то связь обратная. Чем ближе коэффициент к единице, тем теснее связь. Рассмотрим на примере расчет коэффициента Фетнера:
Расчет этого показателя осуществляется вычислением средних значений обоих признаков, а затем определяются знаки отклонения от средней для всех значений взаимосвязанных признаков. С- число совпадений знаков отклонений индивидуальных значений от средней, а Н – число несовпадений знаков. Коэффициент принимает значения от -1 до +1.Если коэффициент имеет знак плюс, то имеется прямая зависимость, если минус, то связь обратная. Чем ближе коэффициент к единице, тем теснее связь. Рассмотрим на примере расчет коэффициента Фетнера:
| Срок службы основных фондов (лет) х | Затраты на ремонт основных фондов (млн. руб.) у | Знак отклонения от средней для х | Знак отклонения от средней для у | Совпадение знаков (С) и несовпадение знаков (Н) |
| 0,5 0,7 0,7 1,1 0,8 1.0 0,6 1,2 1,4 1,5 | - - - - - + + + + + | - - - + - + - + + + | С С С Н С С Н С С С | |
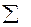 55 55
| 8,9 |
Средний срок службы основных фондов составит 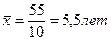 , а средние затраты на ремонт
, а средние затраты на ремонт 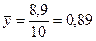 млн. рублей. В последней графе таблицы указаны совпадения и несовпадения знаков отклонений от средних. Подставим их в формулу Фетнера:
млн. рублей. В последней графе таблицы указаны совпадения и несовпадения знаков отклонений от средних. Подставим их в формулу Фетнера:
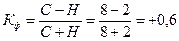 , Полученная величина свидетельствует о том, что между сроком службы основных фондов и затратами на их ремонт существует значительная прямая зависимость.
, Полученная величина свидетельствует о том, что между сроком службы основных фондов и затратами на их ремонт существует значительная прямая зависимость.
Еще один метод нахождения связи между факторами – методом корреляции рангов и, в частности, коэффициент корреляции рангов К. Спирмена 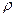 . В основе этого метода лежит рассмотрение разности рангов значений признаков. Формула этого коэффициента:
. В основе этого метода лежит рассмотрение разности рангов значений признаков. Формула этого коэффициента:
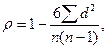 где n - число сопоставляемых пар, d- разность между рангами (порядковыми номерами) в двух рядах. Также как и коэффициент Фетнера этот коэффициент может находится в пределах от -1 до +1.
где n - число сопоставляемых пар, d- разность между рангами (порядковыми номерами) в двух рядах. Также как и коэффициент Фетнера этот коэффициент может находится в пределах от -1 до +1.
На примере часовой заработной платы сотрудников фирмы с различным стажем работы рассмотрим применение коэффициента корреляции рангов Спирмена.
При наличии одинаковых вариантов в рядах распределения ранг для расчета берется как их среднее арифметическое:
| Стаж работы х (лет) | Ранг по порядку | Часовая заработная плата у (руб.) | Ранг по порядку | Ранг х для расчета | Ранг у для расчета | d | d2 |
| 2,5 2,5 | 4,5 4,5 | -2 0,5 -0,5 -1 -1 | 0,25 0,25 | ||||
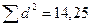
|
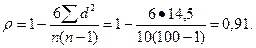
Между стажем и часовой заработной платой установлена тесная корреляционная зависимость.
Преимущество коэффициента рангов Спирмена заключается в том, что он может применяться при любой форме распределения и для любых признаков.
Date: 2015-07-24; view: 361; Нарушение авторских прав