Блок 8. Показатели вариации

Различие индивидуальных значений признака внутри изучаемой совокупности называется вариацией признака. Колеблемость отдельных значений характеризуют показатели вариации. Различают вариацию признака случайную и систематическую. Анализ вариации позволяет оценить ее характер и определить насколько однородной является изучаемая совокупность и насколько характерной является ее средняя величина для данной совокупности.

Выделяют абсолютные и средние показатели вариации. Наиболее простой – размах вариации (R) – разность между наибольшим и наименьшим значением признака в распределении: R= .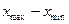

Для получения обобщенной характеристики отклонений от средней рассчитывают среднее линейное отклонение 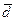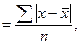для несгруппированных данных и для вариационного ряда 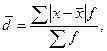показатель учитывается без знака этих отклонений.

На практике вариацию чаще оценивают с помощью показателя дисперсии 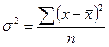в варианте без частот и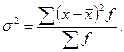

Если из дисперсии извлечь корень квадратный, то получится еще один показатель вариации – среднее квадратическое отклонение:

в варианте без частот и 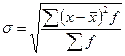в варианте с частотами.

Коэффициент осцилляции характеризует относительную колеблемость крайних значений признака вокруг средней:

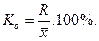
Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины:

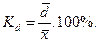
Наиболее распространенный показатель колеблемости, который дает обобщающую характеристику – коэффициент вариации:

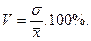
Рассмотрим пример, где оценивается вариация стажа работы по специальности работников двух турфирм:

1-я 2-я

1 4

2 4

3 5

4 5

4 5

9 7

10 7

12 7

45 лет 45 лет

Проведем предварительные расчеты:

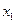
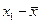
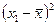
№ пп	Стаж (лет)			Стаж
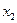
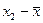
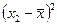
		-4,6 -3,6 -2,6 -1,6 -1,6 3,4 4,4 6,4	21,16 12,96 6,76 2,56 2,56 11,56 19,36 40,96		-1,6 -1,6 -0,6 -0,6 0,4 1,4 1,4 1,4	2,56 2,56 0,36 0,36 0,16 1,96 1,96 1,96
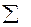
		-	117,88		-	11,88

Сопоставим показатели вариации стажа работников у двух турфирм.

1-я фирма 2-я фирма

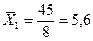
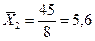
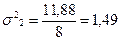
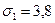
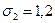
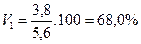
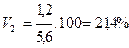
При одинаковых средних величинах стажа работников фирм вариация признака в первой фирме в три раза выше, чем в первой.

Преобразование формулы среднего квадратического отклонения приводит ее к виду 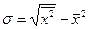, что делает ее удобнее для практических расчетов. Этот показатель широко применяется для расчетов показателей вариации в различных отраслях знания и техники. Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются конкретные варианты от среднего их значения.

Дисперсия альтернативного признака характеризует вариацию альтернативных признаков. Альтернативными признаками являются признаки, которыми обладают одни единицы изучаемой совокупности и не обладают другие. Например, в фирме работают мужчины и женщины, доля мужчин (р) и доля женщин (q) образуют целый коллектив сотрудников фирмы: p +q = 1. Средняя величина для альтернативных признаков равна 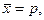а дисперсия . Если на фирме работает 15 мужчин и 20 женщин, то р= 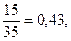а 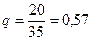, следовательно дисперсия альтернативного признака 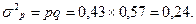Максимальное значение дисперсии альтернативного признака равно 0,25, оно получается при р=0,5.

Правило сложения дисперсий. Если совокупность варьирующих элементов подразделить на несколько групп, то можно выделить: общую дисперсию (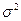), внутригрупповую дисперсию (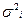), среднюю из внутригрупповых дисперсий (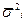), межгрупповую дисперсию ().

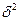Общая дисперсия характеризует колеблемость признака во всей изучаемой совокупности и рассчитывается по формуле:

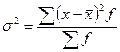, где 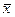- общая средняя для всей совокупности.

Внутригрупповая дисперсия характеризует колеблемость признака внутри группы и рассчитывается по формуле:

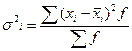, где 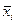- групповая средняя.

Средняя из внутригрупповых характеризует внутригрупповую колеблемость вокруг внутригрупповых средних и рассчитывается как средняя величина из внутригрупповых дисперсий:

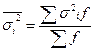, где 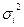- дисперсии отдельных групп, а f - численность отдельных групп.

Межгрупповая дисперсия показывает вариацию групповых средних вокруг общей средней, измеряет вариацию изучаемого признака под влиянием признака - фактора (группировочного признака) и рассчитывается по формуле:

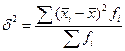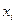, где и 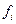- средние и численности по отдельным группам.

Между всеми приведенными дисперсиями существует взаимосвязь, которая называется правилом сложения дисперсий – общая дисперсия равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии:

.

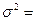
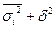Логика этого правила следующая: общая дисперсия, возникающая под влиянием всех факторов, должна быть равна сумме дисперсий, возникающих под влиянием всех прочих факторов, и дисперсии возникающей за счет фактора группировки. Зная два вида дисперсий, всегда можно определить или проверить правильность расчета третьего вида дисперсии. Например, имеются данные по среднедневной выработке сотрудников фирмы с различным стажем работы:

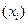
Группы сотрудников по стажу	Число сотрудников (f)	Средняя дневная выработка (т. руб.)	Дисперсия выработки
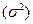
До 5 лет
Более 5 лет

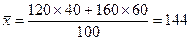т. рублей

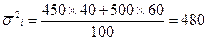
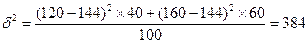, следовательно: .

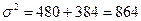В статистике применяется показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии, который показывает, какая часть общей вариации изучаемого признака обусловлена вариацией группировочного признака. Это коэффициент детерминации, рассчитываемый по формуле: .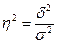

Если извлечь корень квадратный из коэффициента детерминации, получаем новый показатель, который носит название корреляционное отношение:

.

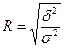Date: 2015-07-24; view: 594; Нарушение авторских прав