Ошибки выборочного наблюдения

При любом наблюдении (сплошном и несплошном) возникают ошибки при регистрации единиц наблюдения. Такие ошибки называются ошибками регистрации. Они могут быть случайными и систематическими, это связано в значительной степени с субъективным фактором, который всегда присутствует при организации и проведении наблюдения.

При проведении выборочных наблюдений, помимо ошибок регистрации, возникают случайные ошибки репрезентативности (представительности), которые возникают в связи с тем, что отобранная для наблюдения часть общей совокупности имеет отличную от генеральной n

Научным обоснованием случайных ошибок выборки являются теория вероятностей и ее предельные теоремы. Используются теоремы русских математиков П.Л. Чебышева и А.М. Ляпунова. В соответствии с этими теоремами, с увеличением численности выборки размеры случайных ошибок сокращаются, что при достаточно большом объеме выборки случайная ошибка будет сколь угодно мала и что характеристики выборочного наблюдения будут надлежащим образом представлять генеральную совокупность.

Возможные расхождения между характеристиками выборочной и генеральной совокупности измеряются средней ошибкой выборки 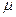. Под средней ошибкой выборки понимают расхождение между средними выборочной и генеральной совокупности (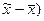, которое не превышает 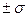. В математической статистике доказано, что значение средней ошибки выборки определяются по формуле:

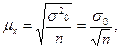где 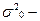дисперсия изучаемого признака х в выборочной совокупности, а n – численность выборочной совокупности.

Соответственно для расчета средней ошибки доли изучаемого признака используется формула:

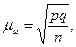где pq – где дисперсия доли изучаемого признака, а n – численность выборочной совокупности. Следовательно, для уменьшения средней ошибки выборки в 3 раза необходимо увеличить объем выборки в 9 раз.

Рассмотрим условный пример. Генеральная совокупность – число сделок N =1000

Доходность сделок (тыс. руб.) Число сделок

12 200

14 500

15 300

Всего: 1000

Средня доходность:

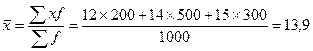тыс. руб.

Дисперсия: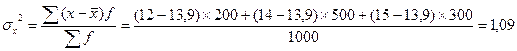

Доля сделок с доходностью 14 и более тыс. рублей р = 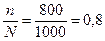или 80%

Предположим, что случайным образом отобрана информация о 200 сделках и получены данные о средних и относительных показателях:

Доходность сделок (тыс. руб.) Число сделок

12 34

14 100

15 66

Всего: 200

Средняя доходность 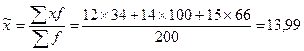тыс. руб.

Дисперсия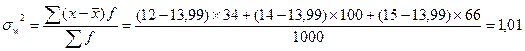

Доля сделок с доходностью 14 и более тыс. рублей w = 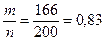или 83%.

Сведем полученные показатели в таблицу:

Теперь можно определить среднюю ошибку выборки:

Для средней доходности ;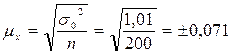

Для доли 14 и более т. руб. .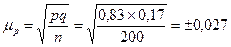

Date: 2015-07-24; view: 346; Нарушение авторских прав