Пример 6.3

Построить эпюры Q_у и М_z для балки с промежуточным (" висячим ") шарниром, изображенной на рис. 13, а.

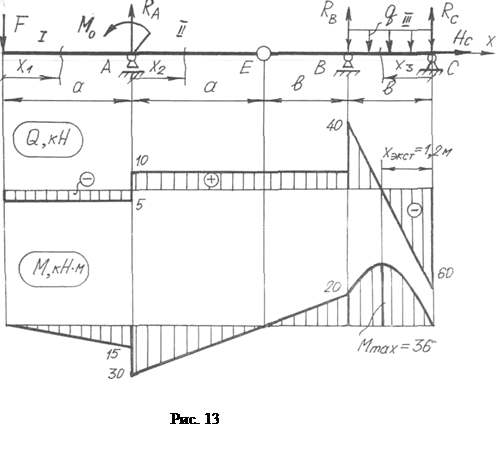
Исходные данные: F = 5 кН; М_о = 15 кНм; q = 50 кН/м; а = 3 м; b = 2 м.

Решение. Особенность балок с промежуточным шарниром заключается в том, что они имеют четыре неизвестные реакции опоры, но их можно определить из уравнений статики, используя дополнительное уравнение равновесия - равенство нулю момента в промежуточном шар­нире.

Σ Х = 0: Н_С = 0.

Из суммы моментов относительно шарнира Е для сил, приложенных только к левой части:

(Σ М_А) _лев = 0: F ×2 а + М_о - R_Aа = 0;

Σ М_В = 0: F (2 a + b) + M_o – R_A (a + b) + R_Сb – qb ² /2 = 0;

R_С = [ R_A (a + b) + qb ² /2 – F (2 a + b) - M_o ]/ b = [15(3 + 2) + 50×2²/2 -5(2×3+2)-15]/2 = 60 кH;

(Σ М_А) _пр = 0: R_С 2 b + R_Bb - qb (b + b /2) = 0;

R_B = [ qb (b + b /2) - R_C 2 b ]/ b = [50×2(2+2/2)- 60×2×2]/2 = 30 кH.

Проверка правильности определения реакций:

Σ Y = 0: R_А + R_B + R_C – F – qb = 15 + 70 + 60 – 5 - 50×2 = 0.

Реакции вычислены верно.

Для построения эпюр Q_у и М_z балку разбиваем на три участка (см. рис13, а).

Первый участок: 0 ≤ x ₁ ≤ a:

Из условия равновесия левой отсеченной части:

при x ₁ = а: Q₁ = - 5 кН; М ₁ = - Fа = -5×3 = - 15 кНм.

Второй участок: 0 ≤ x ₂ ≤ (a + b):

Из условия равновесия левой отсеченнойчасти:

Q₂ = - F + R_A = - 5 + 15 = 10 кН;

М₂ = - F (а + x ₂) - М_о + R_A x ₂.

На участке, где расположен шарнир, рекомендуется вычислять момент в шарнире для проверки правильности вычислений. Момент в шарнире должен быть равен нулю:

при x ₂ = 0: Q₂ = 10 кН; М₂ = - Fа - М_о = - 30 кНм;

при x ₂ = а (в шарнире): Q₂ = 10 кН;

М₂ = - F ×2 а - М_о + R_Aа = -5×2×3 -15+ 15×3 = 0.

при x ₂ = а + b: Q₂ = 10 кН;

М₂ = - F (2 а+b) - М_о + R_A (а+b) = -5(2×3+2) - 15+ 15(3+2)=20 кНм.

Третий участок: 0 ≤ x ₃ ≤ b:

Рассматриваем равновесие правой отсеченной части:

Q₃ = - R_С +qх₃; М₃ = R_С х₃ – q х₃ ²/2;

при х₃ = 0: Q₃ = - R_С = - 60 кН; М₃ = 0;

при х₃ = b: Q₃ = - R_С + qb = - 60 + 50×2 = 40 кН;

М₃ = R_С b-qb²/ 2 = 60×2 - 50 ×2²/2 = 20 кНм.

На этом участке эпюра Q_у пересекает ось, поэтому необходимо определить М_экстр, как и в примере 6.2. Из условия Q₃ = 0 находим координату х_экстр:

- R_C + qx_3экстр = 0; x_3экстр = R_C / q = 60/50 = 1,2 м;

M_экстр = R_C x_3экстр – qx ² _3экстр /2 = 60×1,2 – 50×1,2²/2 = 36 кHм.

По полученным значениям строим эпюры Q_у и М_z (рис. 13, б).

Date: 2015-07-24; view: 865; Нарушение авторских прав