Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Пример 6.2
|
|
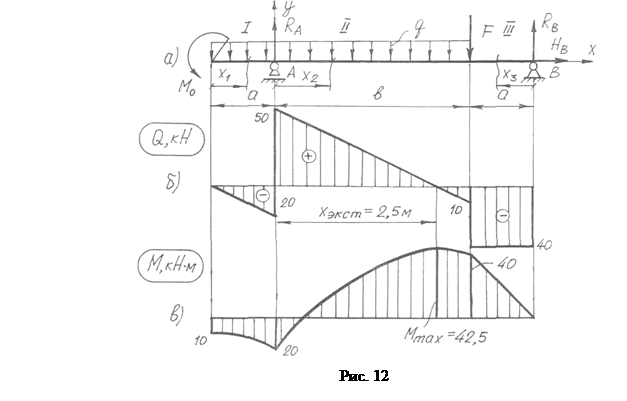
Построить эпюры Qу и Мz для балки на двух опорах, изображенной на рис. 12, а.
Исходные данные: Mo = 10 кHм; F = 30 кН; q = 20 кH/м; а = 1 м; b = 3 м.
Решение. До построения эпюр необходимо из уравнений равновесия определить реакции опор:
Σ Х = 0; НВ = 0.
Σ МВ = 0; Мо + q (a + b)[ a + (a+b)/2] + F×a – RА (a + b) = 0.
RА = Мо /(a+b) + q [ a + (a+ b)/2] + F×a /(a + b) = 10/(1+3) + 20[1 + (1+3)/2] + 30 × 1/(1+ 3) = 70 кH.
Σ МА = 0; Mo + qa2 /2 – qb2 /2 – Fb + RВ (a + b) = 0.
RВ = - Мо /(a+b) - q a 2[(a+ b)2] + qb 2/[2(a + b)] + F×b /(a+b) = - 10/(1+3) - 20 × 12 /[2(1+3)] +20 × 32 /[2(1+3)] +20 × 3 /(1+3) = 40 кH.
Проверка правильности определения реакций:
Σ Y = 0: RА + RВ - F - q (а + b) = 70 + 40 - 30 - 20(1+3) = 0.
Реакции определены верно.
Для построения эпюр балку разбиваем на три участка (см. рис. 12, а)
Первый участок: 0 ≤ x 1 ≤ а:
Из уравнений равновесия левой отсеченной части получаем:
Q1= - qx1 - уравнение наклонной прямой;
М1 = - Mо - q x12 /2 - уравнение параболы.
В начале участка при x1 = 0: Q Q1 = 0; М1 = - Мо = -10 кНм.
В конце участка при x1 = а: Q1 = - qа = - 20 × 1 = - 20 кН;
М1 = - Мо - qа2 /2 = - 10 - 20 × 12/2 = - 20 кНм.
Промежуточные точки параболы можно не вычислять, а используя правило 2 п. 5 провести ее приближенно, направляя выпуклость вверх, против стрелок распределенной нагрузки q.
Второй участок: 0 ≤ x 2 ≤ b:
Рассматривая равновесие левой отсеченные части, получим:
Q2 = - q (a + x 2) + RА - уравнение наклонной прямой;
M2 = - Mo – q (a + x 2)2/2 + RА x 2 - уравнение параболы.
Определяем характерные ординаты:
при x 2 = 0: Q2 = - qa + RА = -20 + 70=50 кН;
M2 = - Mo – qa 2/2 = - 10 - 20 × 12/2 = - 20 кНм;
при x 2 = b; Q2 = - q (a+b) + RА = - 20(1 + 3) + 70 = -10 кН;
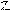M2 = - Mo – q (a + b)2/2 + RА b = - 10 -20 (1+3)2/2 + 70 × 3 = 40 кHм.
По полученным значениям строим эпюру Qу (рис. 12, б), а для построения эпюры Мz требуется еще дополнительно определить координату сечения, в котором возникает Мэкстр и его величину, таккак эпюра Qу на этом участке плавно переходит через нуль (см. правило 4 п. 5).
Методика определения Мэкстр.
Определяем координату сечения, в котором возникает Мэкстр,из условия, что поперечная сила в этом сечении равна нулю:
Q2 = 0: - q (а + х2экстр) + RА = 0,
х2экстр = RА / q - a = 70/20 – 1 = 2,5 м.
Величину М2экcтр получаем, подставляя в уравнение М2 координату х2экстр:
М2экcтр = - Mo - q (а + х2экстр)2/2 + RА х2экстр = - 10 – 20 (1+ 2,5)2/2 + 70 × 2,5 = 42,5 кHм.
Третий участок: 0 ≤ x 3 ≤ a:
На этом участке рациональнее рассматривать равновесие правой отсеченной части, так как на нее действует меньше нагрузок и уравнения будут проще:
Q3 = - RВ - уравнение прямой, параллельной оси,
М3 = RВх3 - уравнение наклонной прямой.
Характерные ординаты:
при х3 = 0; М3 = 0;
при х3 = а: М3 = RВа = 40 × 1 = 40 кНм.
Q3 = - 40 кН в любом сечении третьего участка, так как не зависит от текущей координаты х3.
По полученным значениям построены эпюры Qу (рис. 12, б) и Мz (рис. 12, в).
Date: 2015-07-24; view: 453; Нарушение авторских прав