
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема Штейнера
|
|
Из определения момента инерции тел в общем виде:
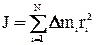 (30)
(30)
следует, что эта величина является аддитивной. Это означает, что моменты инерции тел в некоторых случаях можно найти интегрированием исходя из геометрических соображений.
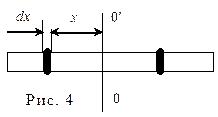 В качестве примера найдём момент инерции J тонкого стержня длиной l, массой m и диаметром d << l относительно оси
В качестве примера найдём момент инерции J тонкого стержня длиной l, массой m и диаметром d << l относительно оси 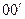 проходящей через его центр масс перпендикулярно к стержню (Рис. 4). Выделим на расстоянии х от оси вращения элемент стержня бесконечно малой толщины d x.
проходящей через его центр масс перпендикулярно к стержню (Рис. 4). Выделим на расстоянии х от оси вращения элемент стержня бесконечно малой толщины d x.
Масса этого элемента dm = r×S×d x, где r – плотность материала, S – площадь поперечного сечения. Момент инерции элемента массы dm:
 () Учитывая, что элементы массы dm попарно симметричны относитель-
() Учитывая, что элементы массы dm попарно симметричны относитель-
но оси вращения 00', проинтегрируем левую часть () в пределах от 0 до J, а правую в пределах от 0 до l /2. Получим:
 ()
()
Т.к. 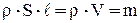 – масса стержня, то окончательно для тонкого стержня
– масса стержня, то окончательно для тонкого стержня
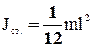 (33)
(33)
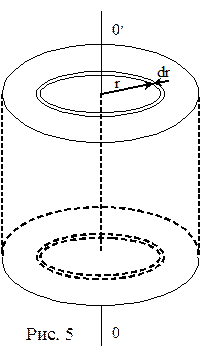 Определим момент инерции диск или цилиндра радиусом R, высотой h и массой m относительно его геометрической оси, параллельной образующей. Выделим цилиндрический слой бесконечно малой толщины dr и радиусом r. Очевидно, что все элементы этого слоя будут иметь одинаковые моменты инерции. Это, значит, что момент инерции слоя
Определим момент инерции диск или цилиндра радиусом R, высотой h и массой m относительно его геометрической оси, параллельной образующей. Выделим цилиндрический слой бесконечно малой толщины dr и радиусом r. Очевидно, что все элементы этого слоя будут иметь одинаковые моменты инерции. Это, значит, что момент инерции слоя
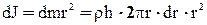 .
.
Т.к. r изменяется в пределах от r = 0 до r = R, то интегрируя получим:
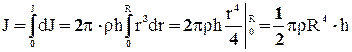
но 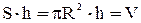 ,
, 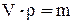
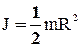 (36)
(36)
Без выводов запишем:
а) шар радиусом R и массой m, относительно оси, проходящей через его центр – 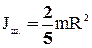 (31)
(31)
б) полый тонкостенный цилиндр радиусом R и массой m, относительно его геометрической оси, параллельной образующей –
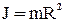 (32)
(32)
Согласно теореме Штейнера момент инерции тела – J относительно любой оси, параллельной оси проходящей через центр масс этого тела –
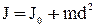 , (33)
, (33)
где J0 – момент инерции тела относительно оси, проходящей через центр масс, d – расстояние между осями. Например, если ось вращения проходит через конец стержня,
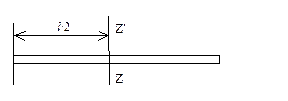 |
то 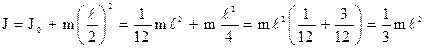 (34)
(34)
В качестве примера Определим момент инерции J тонкого стержня длиной l, массой m и диаметром d<< l. Относительно оси 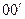 к перпендикулярной
к перпендикулярной
а) тонкий однородный стержень.
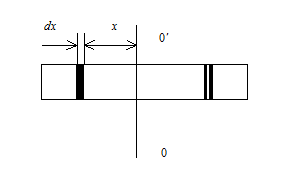 к стержню и проходящей через его центр масс.
к стержню и проходящей через его центр масс.
Выделим на расстоянии х от оси вращения элемент стержня бесконечно малой толщины d x.
Масса этого элемента dm = r×S×d x, где r-плотность материала,
S-площадь поперечного сечения. Момент инерции элемента массы dm
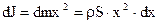
Интегрируем левую и правую части в пределах от 0 до J и правую от 0 до l /2. Учитывая, что элементы попарно симметричны, получим:
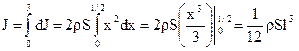
Т.к. 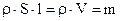 , то окончательно
, то окончательно 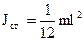 (33)
(33)
б) диск или цилиндр радиусом R, высотой h и массой m.
Определим момент инерции цилиндра относительно его геометрической оси, параллельной образующей.
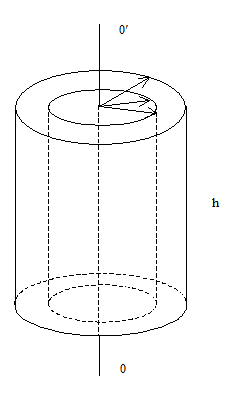 Выделим цилиндрический слой бесконечно малой толщины dr и радиусом r. Очевидно, что все элементы этого слоя будут иметь одинаковые моменты инерции. Это, значит, что момент инерции слоя
Выделим цилиндрический слой бесконечно малой толщины dr и радиусом r. Очевидно, что все элементы этого слоя будут иметь одинаковые моменты инерции. Это, значит, что момент инерции слоя
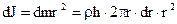 .
.
Т.к. r изменяется в пределах от r = 0 до r = R, то интегрируя получим:
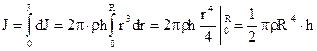
но 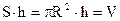 ,
, 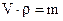
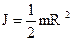 (36)
(36)
Без выводов запишем:
а) тонкий однородный стержень –
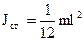 (31)
(31)
б) диск или цилиндр радиусом R, высотой h и массой m -
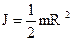 (32)
(32)
Согласно теореме Штейнера момент инерции тела - J относительно любой оси, параллельной оси проходящей через центр масс этого тела
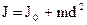 , (33)
, (33)
где J0 – момент инерции тела относительно оси через центр масс, d - расстояние между осями. Например, если ось вращения проходит через конец стержня,
 |
то 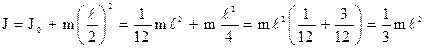 (34)
(34)
В качестве примера найдём момент инерции J тонкого стержня длиной l, массой m и диаметром d<< l. Относительно оси 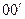 к перпендикулярной
к перпендикулярной
а) тонкий однородный стержень.
 к стержню и проходящей через его центр масс.
к стержню и проходящей через его центр масс.
Выделим на расстоянии х от оси вращения элемент стержня бесконечно малой толщины d x.
Масса этого элемента dm = r×S×d x, где r-плотность материала,
S-площадь поперечного сечения. Момент инерции элемента массы dm
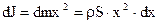
Интегрируем левую и правую части в пределах от 0 до J и правую от 0 до l /2. Учитывая, что элементы попарно симметричны, получим:
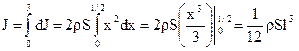
Т.к. 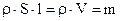 , то окончательно
, то окончательно 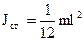 (33)
(33)
 б) диск или цилиндр радиусом R, высотой h и массой m.
б) диск или цилиндр радиусом R, высотой h и массой m.
Определим момент инерции цилиндра относительно его геометрической оси, параллельной образующей.
Выделим цилиндрический слой бесконечно малой толщины dr и радиусом r. Очевидно, что все элементы этого слоя будут иметь одинаковые моменты инерции. Это, значит, что момент инерции слоя
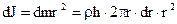 .
.
Т.к. r изменяется в пределах от r = 0 до r = R, то интегрируя получим:
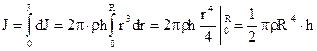
но 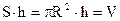 ,
, 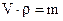
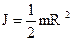 (36)
(36)
Без выводов запишем:
а) тонкий однородный стержень –
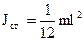 (31)
(31)
б) диск или цилиндр радиусом R, высотой h и массой m -
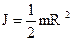 (32)
(32)
Согласно теореме Штейнера момент инерции тела - J относительно любой оси, параллельной оси проходящей через центр масс этого тела
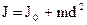 , (33)
, (33)
где J0 – момент инерции тела относительно оси через центр масс, d - расстояние между осями. Например, если ось вращения проходит через конец стержня,
 |
то 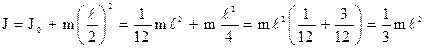 (34)
(34)
Без выводов запишем:
а) тонкий однородный стержень – ДОПОЛНИТЬ ВЫВОДОМ
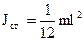 (31)
(31)
б) диск или цилиндр радиусом R, высотой h и массой m -
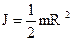 (32)
(32)
Согласно теореме Штейнера момент инерции тела - J относительно любой оси, параллельной оси проходящей через центр масс этого тела
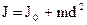 , (33)
, (33)
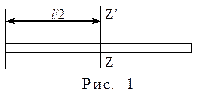 где J0 – момент инерции тела относительно оси через центр масс, d - расстояние между осями. Например, для стержня, если ось вращения проходит через его конец (рис.1):
где J0 – момент инерции тела относительно оси через центр масс, d - расстояние между осями. Например, для стержня, если ось вращения проходит через его конец (рис.1):
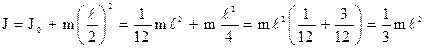 (34)
(34)
Date: 2015-07-24; view: 448; Нарушение авторских прав