Вращательное движение

ЛЕКЦИЯ № 2

КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ.

Простейшей формой движения материи является механическое движение. Оно представляет собой изменение положения тела или его отдельных частей в пространстве, т.е. относительно друг друга. Основная задача механики состоит в ответе на вопрос: где будет находиться тело в интересующий нас момент времени.

Любое движение в механике может быть представлена как комбинация двух основных видов движения: поступательного и вращательного.

Рассмотрим наиболее простой случай вращательного движения: вращение абсолютно твердого тела вокруг неподвижной оси.

Тело называется абсолютно твердым, если расстояние между его любыми двумя точками неизменно. Понятно, что это понятие является физической абстракцией. Реально этому условию удовлетворяют тела, деформациями которых при решении тех или иных задач можно пренебречь.

При вращении разные точки твёрдого тела движутся по окружностям, центры которых образуют прямую. Эта прямая и называется осью вращения. Легко заметить, что угловые перемещения всех точек за один и тот же промежуток времени Dt будут при этом одинаковыми. По этой причине положение вращающегося тела целесообразно определять углом, на который оно поворачивается относительно своего начального положения. Уравнением вращательного движения в этом случае будет функция j = f(t), которая будет иметь один и тот же вид для всех точек тела. Получим выражение этой функции в общем виде. Для этого достаточно рассмотреть движение одной из точек тела вокруг оси.

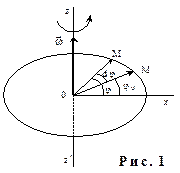Пусть твердое тело вращается вокруг оси 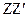. Траектория движения точки М будет представлять собой окружность, плоскость которой перпендикулярна 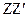, а центр 0 лежит на этой прямой. Положение произвольной точки М на траекто-рии будем определять углом j, который образует радиус-вектор 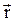, проведенный из центра окружности к точке М, с лучом 0 х, лежащим в плоскости траектории и выбранным за начало отсчета.

В СИ измерение угла j производится в радианах. Угол в 1 радиан – это центральный угол, который опирается на дугу длинной равной радиусу окружности r. Т.е., чтобы определить угол в радианах надо длину дуги разделить на её радиус кривизны:

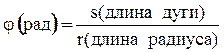(1)

Рассмотрим основные кинематические параметры вращательного движения. Пусть за бесконечно малый промежуток времени dt материальная точка из положения М переместится в положение 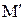, пройдя путь ds. При этом радиус-вектор 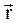повернётся на бесконечно малый угол dj.

Угловая скорость w – это вектор численно равный углу поворота радиус-вектора 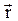за единицу времени и направленный так, что с его острия движение точки совершается против часовой стрелки. Начало 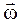находится в точке О.

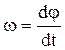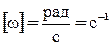. . (2)

Время, за которое тело совершает один полный оборот, называется периодом вращения (Т). Т.к. угол поворота, соответствующий одному полному обороту Dj = 2p рад, то при равномерном движении

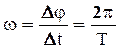. (3)

Величину равную числу оборотов тела за единицу времени называют частотой вращения n:

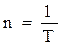; . (4)

Уравнение равномерного вращательного движения (ω = const) получим, решив дифференциальное уравнение (2):

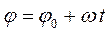. (5)

При неравномерном вращении быстрота изменения угловой скорости характеризуется угловым ускорением b:

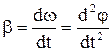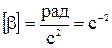. . (6)

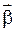– это вектор, расположенный на оси вращения и направленный, так как и 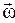, если скорость растет, и в противоположном направлении, если скорость уменьшается.

В общем случае, уравнение равноускоренно вращательного движения (β = const) можно получить, решив дифференциальное урав-

нение (6) относительно j:

w = w₀ + bt, (7)

(8).

Для описания движения по круговой траектории можно использовать и уже знакомые нам линейные кинематические параметры. Например, скорость движения точки по траектории:

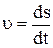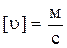. . (9)

Эта скорость при переходе из одной точки траектории (М) в другую (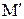) будет меняться в общем случае как по величине, так и по направлению (рис.2):

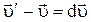(10)

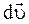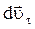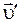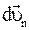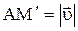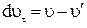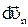Разложим вектор на две составляющие: – направленную вдоль и – проведенную так, что . Из чертежа видно, что du_τ –равна приращению модуля скорости , а определяет изменение направления вектора скорости 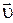при переходе точки тела из положения М в .

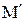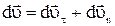(11).

Разделив (11) на dt, получим:

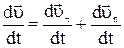(12)

Так как 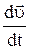– это полное линейное ускорение 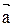, то (12) перепишется

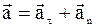, (13) где 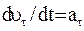– тангенциальное ускорение, которое характеризует быстроту изменения скорости по величине (по модулю); du_n/dt = a_n – нормальное ускорение, которое определяет „быстроту” изменения направления скорости.

Установим взаимосвязь линейных и угловых параметров движения по окружности. Из соотношения (1)

s = j × r. (14)

Продифференцировав правую и левую часть по t, имеем:

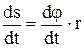, т.е. u = w×r. (15)

Эта формула определяет взаимосвязь модуля линейной скорости u и модуля угловой скорости b. Дифференцируем (15) еще раз по t, получим для тангенциального ускорения:

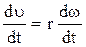, а_t = r×b. (16)

Из треугольника 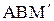при радианной мере малых углов:

du_n = u·sindj = u·dj. Но 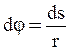, тогда .

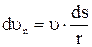Дифференцируя по t правую и левую часть последнего равенства, получим:

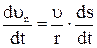отсюда 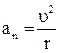. (17)

Учитывая (15), из (17) получим:

a_n = w²r (18)

Из D АВС (dυ)² = (dυ_τ)² + (dυ_n)² или после деления на (dt)² – 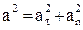. С учетом (16) и (18)

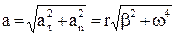. (19)

Date: 2015-07-24; view: 361; Нарушение авторских прав