
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные временные характеристики электрических сигналов
|
|
Каждый класс сигналов имеет свои особенности и требует специфических методов описания и исследования. Поэтому в теории связи каждому классу сигналов соответствует свое математическое представление, своя математическая модель.
Математической моделью сигнала называют систему математических соотношений, описывающих изучаемый процесс или явление (описание с помощью математических объектов (функций, векторов, распределений и т.д.), позволяющее делать выводы об особенностях сигнала). Целью математического описания является разработка математических моделей сообщений, сигналов и помех, необходимых для анализа, синтеза и оптимизации объектов информационной техники. Математические модели позволяют анализировать свойства сообщений, сигналов и помех, а также синтезировать сигналы с требуемыми свойствами.
Функции, описывающие сигналы, могут принимать как вещественный, так и комплексный вид.
Наиболее распространенными способами представления (описания) сигналов являются спектральное и временное. Описание сигнала некоторой функции времени полностью определяет его свойства. Колебание может быть представлено либо графически, либо аналитической зависимостью. В отдельных случаях график дает все необходимые сведения о сигнале.
Однако чаще всего применение графиков затруднительно и удобнее пользоваться аналитическим описанием колебаний - временным, либо частотным (спектральным).
При временном описании колебание U(t) выражается как функция времени или как сумма более простых временных функций.
Например,
| U(t)= at2, или U(t) = а1 - а2t. | (1) |
При спектральном описании U(t) представляют в виде суммы составляющих различных частот. Например:
| U(t) = Um1 сosW1t + Um2 сosW2t | (2) |
В теории связи широко используется представление сложных сигналов в
виде совокупности гармонических функций:
| U(t) = Um сos(wt+j0) | (3) |
каждая из которых характеризуется своими амплитудой Um; циклической частотой w=2pf; начальной фазой j0.
Кроме упомянутых представлений используются представления сигналов в виде таблиц, что позволяет говорить о табличном и статистическом представлениях.
Для характеристики основных свойств сигналов обычно используют временные характеристики, энергетические характеристики, характеристики сигналов как случайного процесса.
а) временные характерист ики.
Допустим, имеем гармонический сигнал:
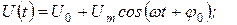
| (4) |
временными характеристиками которого являются:
- U0 – постоянная составляющая;
- Um – переменная составляющая амплитуды колебания;
- 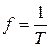 - линейная частота;
- линейная частота;
- j0 – начальная фаза;
-  - угловая (циклическая) частота.
- угловая (циклическая) частота.
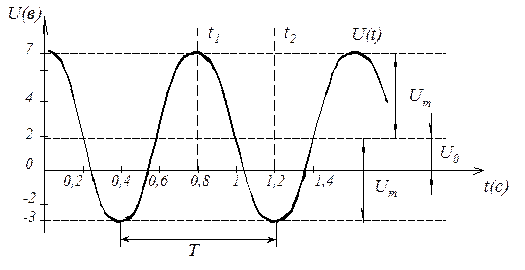
Рис. 1. Временное представление гармонического колебания (4)
U0 = 2В, Um = 5B, j0 = 0, T = 1,2-0,4=0,8; 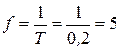 ;
;
таким образом, U(t)= 2 + 5 cos( 1,25 . 2 p t + 0 )= 2 + 5 cos 2,5 p t.
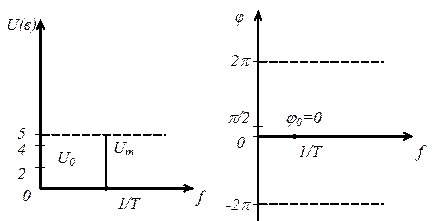
Рис. 2. Спектральное представление гармонического колебания (4)
б) энергетические характеристики сигналов.
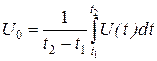 — постоянная составляющая; — постоянная составляющая;
| (5) |
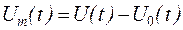 — переменная составляющая; — переменная составляющая;
| (6) |
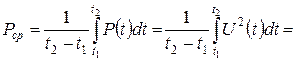 — средняя мощность; — средняя мощность;
| (7) |
или 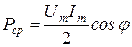 - для гармонического колебания; - для гармонического колебания;
| (8) |
P(t)= i(t)U(t)cosj - мгновенная мощность;
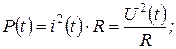 - мгновенная мощность;
- мгновенная мощность;
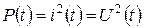 -мгновенная мощность, выделяемая на сопротивление в 1 Ом.
-мгновенная мощность, выделяемая на сопротивление в 1 Ом.
Действующие значения напряжения и тока.
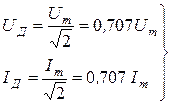 - для гармонического колебания - для гармонического колебания
| (9) |
Пикфактор - 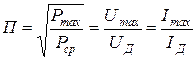 , ,
| (10) |
для гармонического колебания 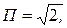 для речи П = 5 ¸ 6.
для речи П = 5 ¸ 6.
в) характеристики сигналов как случайного процесса (вероятностные характеристики).
Все реальные сигналы не являются детерминированными. Их нельзя описать с помощью функции времени. Требуется ввести вероятностные характеристики.
Отличительной чертой детерминированного сигнала является то, что, задавая момент времени t можно точно предсказать значение сигнала в этот момент. У недетерминированного сигнала значение его меняется случайным образом, и предсказать его точно невозможно. Любой недетерминированный сигнал можно представить последовательной реализацией.
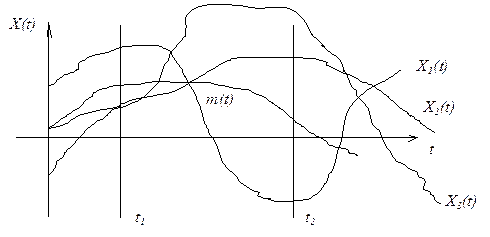
Рис. 3. Временные диаграммы недетерминированных сигналов
Под случайным процессом X(t) будем понимать поток случайных величин, которые отсчитывают поведение этого процесса во времени.
Случайные процессы характеризуются: математическим ожиданием; дисперсией; функцией корреляции.
Date: 2015-07-24; view: 1217; Нарушение авторских прав