Классификация отображений

Пусть X и Y - два частично упорядоченных множества.

Отображение ц множеств X на Y есть изоморфизм (или изоморфное отображение), если оно взаимно однозначно и сохраняет порядок, то есть неравенства х ≤ у и ц(х) ≤ ц(у) равносильны.

Обратное отображение ц^-1 есть также изоморфизм.

В случае существования изоморфизма частично упорядоченные множества называются изоморфными. Изоморфные частично упорядоченные множества обычно отождествляют, поскольку с точки зрения свойств, связанных с порядком, они неразличимы.

Отображение ц называется изотопным, если неравенство х ≤ у влечет ц(х) ≤ ц(у). Изоморфное отображение всегда изотонно (но не наоборот!).

Взаимно однозначное отображение ш множества X на Y называется дуальным изоморфизмом, если равносильны неравенства х ≤ у и ц(х) ≥ ц(у). Если такое отображение существует, то говорят, что X и Y дуально изоморфны.

Операция

Частным случаем п -местной функции у = F(х₁, х₂,..., х_n) является п - местная операция. Под п-местной операцией O_n в множестве М понимается п -местная функция у = F(х₁, х₂,..., х_n), у которой области определения аргументов и область значений функции совпадают: М₁ = М₂ =... = М_n = М_у. Таким образом, п -местная операция по п элементам множества М определяет (п + 1) -й элемент этого жемножества.

Алгебраической n-арной (n-местной) операцией на множестве M называется n -местная функция у = f(x₁,x₂,...,x_n), у которой область определения аргументов x_i и область значений функции совпадают (n N).

Пояснение.

1. Тот факт, что алгебраическая операция является частным случаем бинарного однозначного соответствия, отражается в её формальной записи f: Mⁿ 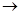M., т.е.:

2. Поскольку алгебраическая операция по n элементам множества M определяет (n+1) элемент этого же множества M, то n -местную алгебраическую операцию можно рассматривать и как (n+1)- арное однозначное отношение на множестве M.

3. Если f: M 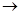M, то говорят об унарной (одноместной) алгебраической операции; если f: M² 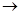M, то имеют в виду бинарную (двухместную) алгебраическую операцию.

Date: 2015-07-24; view: 783; Нарушение авторских прав