
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Суперпозиция бинарных отношений
|
|
Если f: Х 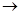 Y, а g: Y
Y, а g: Y 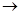 Z, то функция F: X
Z, то функция F: X 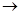 Z, определенная для каждого
Z, определенная для каждого 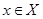 формулой F(х) = g(f(х)), называется композицией (суперпозицией) функции f и g, или сложной функцией.
формулой F(х) = g(f(х)), называется композицией (суперпозицией) функции f и g, или сложной функцией.
Композиция
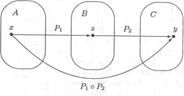 Произведением бинарных отношений Р1
Произведением бинарных отношений Р1 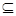 A
A  B и Р2
B и Р2 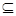 B
B  C или композицией Р1 и Р2 называется множество Р1
C или композицией Р1 и Р2 называется множество Р1  Р2 = {<x,y>|x
Р2 = {<x,y>|x  A, y
A, y  C, и найдется элемент z
C, и найдется элемент z  В такой, что <x,z>
В такой, что <x,z>  P1 и <z,y>
P1 и <z,y>  P2} (рис. 1). В дальнейшем произведение Р1
P2} (рис. 1). В дальнейшем произведение Р1  Р2 будем также обозначать через Р1Р2.
Р2 будем также обозначать через Р1Р2.
Предложение. Для любых бинарных отношений Р, Q, R выполняются следующие свойства:
1) ( P-1)-1 = Р;
2 ) (Р  Q)-1 = Q-1
Q)-1 = Q-1  Р-1;
Р-1;
3) (Р  Q)
Q)  R = Р
R = Р  (Q
(Q  R) (ассоциативность композиции).
R) (ассоциативность композиции).
Доказательство.
1. По определению обратного отношения условие (х,у)  Р равносильно условию (у,х)
Р равносильно условию (у,х)  Р-1, что в свою очередь выполняется тогда и только тогда, когда (х,у)
Р-1, что в свою очередь выполняется тогда и только тогда, когда (х,у)  (Р-1)-1. Следовательно, Р = (Р-1)-1.
(Р-1)-1. Следовательно, Р = (Р-1)-1.
2. Предположим, что (х,у)  (Р
(Р  Q)-1. Тогда (у,х)
Q)-1. Тогда (у,х) 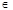 (Р
(Р  Q) и, следовательно, (y,z)
Q) и, следовательно, (y,z) 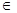 Р и (z,x)
Р и (z,x)  Q для некоторого элемента z. Значит, (x,z)
Q для некоторого элемента z. Значит, (x,z)  Q-1, (z,y)
Q-1, (z,y) 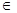 Р-1 и (х,у)
Р-1 и (х,у)  Q-1Р-1. Включение Q-1
Q-1Р-1. Включение Q-1  Р-1
Р-1 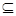 (Р
(Р  Q)-1 доказывается аналогично.
Q)-1 доказывается аналогично.
3. Пусть (х,у)  (Р
(Р  Q)
Q)  R. Тогда для некоторых u и v имеем (x,и)
R. Тогда для некоторых u и v имеем (x,и)  Р, (и,v)
Р, (и,v)  Q, (v,y)
Q, (v,y)  R. Таким образом, (и,у)
R. Таким образом, (и,у)  Q
Q  R и (x,y)
R и (x,y)  Р
Р  (Q
(Q  R).
R).
Включение Р  (Q
(Q  R)
R) 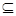 (Р
(Р  Q)
Q)  R доказывается аналогично.
R доказывается аналогично.
Ассоциативность композиции позволяет обозначать композицию (Р  Q)
Q)  R = Р
R = Р  (Q
(Q  R) через PQR. По этой же причине однозначно определена композиция P1P2 … Pn двухместных предикатов P1, P2 ,…,Pn. Отметим, что существуют предикаты Р и Q для которых не выполняется закон коммутативности (приведите примеры таких предикатов).
R) через PQR. По этой же причине однозначно определена композиция P1P2 … Pn двухместных предикатов P1, P2 ,…,Pn. Отметим, что существуют предикаты Р и Q для которых не выполняется закон коммутативности (приведите примеры таких предикатов).
Date: 2015-07-24; view: 1844; Нарушение авторских прав