Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Р2A,B (<а,b>) ↔ b
|
|
Переменную х называют аргументом функции, а у — ее значением. Значок f интерпретируется, как правило, преобразования аргумента х в значение у, т.е. представляет собой способ реализации соответствия. Этот способ может быть задан аналитически (формулой), в виде таблицы, графика или специальной вычислительной процедурой. Важно только то, что для каждого значения хХ он должен давать одно и только одно значение у = f(х).
Функция многих переменных у=f(х1, х2, …, хn) вводится аналогично. Пусть задано множество Х1 
Х2 ... Хn. Тогда, если любому упорядоченному набору <х1, х2,..., xn>ÎХ1 Х2 ... Хn по определенному правилу f поставлено в соответствие число у=f(х1, х2, …, хn), то говорят, что на множестве Х1 Х2 ... Хn определена функция многих переменных f(х1, х2, …, хn).
Рассматривая вместо числовых множеств Х1 Х2 ... Хn множества любой природы, приходим к самому общему определению функции. Пусть М и N — два произвольных множества.
Если каждому элементу хÎМ по некоторому правилу поставлен в соответствие один и только один элемент уÎN, то на множестве М определена функция f, принимающая значения из множества N.
Вместо термина «функция» часто употребляют термин «отображение», понимая под ним отображение одного множества в другое. В данном случае имеем отображения одного множества М в множество N. Записывают это так: f:М→N.
Представление функции в терминах отношений.
Функцией называется бинарное отношение f, если из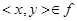 
и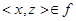 
следует, что y = z.
Подмножество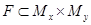 
, называется функцией, если для каждого элемента 
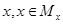, найдется не более одного элемента 
вида 
; при этом если для каждого элемента х имеется один элемент у вида , то функция называется всюду (полностью) определенной, в противном случае — частично определенной (недоопределенной).
Множество Мx образует область определения функции F, множество Му — область значений функции F. Часто вместо записи используют запись у = F(х); при этом элемент х называют аргументом или переменной, а у — значением функции F.
Пусть X, Y - некоторые множества. Говорят, что задана функция (отображения), действующая из множества X во множество Y, если задан закон или правило f, по которому каждому элементу x из множества X ставится в соответствие единственный элемент y из Y: y = f(x).
Пример. Пусть X = R (все вещественные числа) и Y = [-1; 1]. Рассмотрим функцию y = sin x. Каждому элементу из X поставлен в соответствие элемент из Y: пусть x = р/2, тогда y = sin р/2 = 1.
Множество Y называется множеством значений функции f. Элемент y = f(x) 
Y называют образом элемента x при отображении f. Элемент x - прообраз элемента y под действием отображения f. Множество X называется множеством прообразов отображения f.
Пример. Для функции y = sin x: x = R - множество прообразов; Y:=[-1; 1] - множество значений функции; y = 1 - образ x = р/2 при данном отображении (y = sin р/2 = 1), x = р/2 - прообраз элемента y = 1 при данном отображении.
Сопоставим с декартовым произведением двух множеств прямоугольную решетку, узлы которой взаимно однозначно соответствуют элементам декартова произведения. Подмножество декартова произведения на рисунках будем отмечать штриховкой соответствующих элементов.
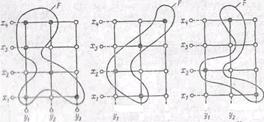Пример 1.1. На рис. 1.2, а изображено подмножество декартова произведения множеств Мx = {х1, х2, х3, х4} и Му = {у1, у1, у3}, не являющееся функцией; на рис. 1.2, б,-являющееся полностью определенной функцией; на рис. 1.2,в — частично определенной функцией.
Количество аргументов определяет местность функции. Выше были рассмотрены одноместные функции. Аналогично понятию декартова произведения двух множеств определим декартово произведение п множеств.
Если множество Мx в определении функции у = F(х) является декартовым произведением множеств Мx1, Мx2,..., Мxn, то получаем определение п-местной функции
у = F(х1, х2,..., хn).
Две функции f и g равны, если они состоят из одних и тех же элементов. Область определения функции и область ее значений задается так же, как и для бинарных отношений. Если область определения дf = Х и область значений сf 
Y, то говорят, что функция f задана на множестве Х со значениями во множестве Y, при этом f отображает множество Х во множество Y. Это отображение обозначается как f: Х 
Y.
Если f — функция, то вместо 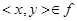пишут y = f(х) и говорят, что y — значение, соответствующее аргументу х, или у — образ элемента х при отображении f. При этом х называют прообразом элемента у.
Назовем f — n - местной функцией из Х в Y, если f: Х 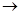Y. Тогда записываем y = f(х1, … хn) и говорим, что у — значение функции при значении аргументов х1, … хn.
Если функция (отображение) f сопоставляет каждому элементу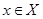 
элемент 
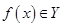, то будем писать f: Х 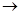Y (такая функция может трактоваться как отношение 
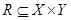с тем свойством, что для каждого 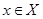существует в R точно одна пара вида <х,y>, 
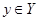; для наших же целей достаточно интуитивного понятия функции).
Отношение R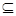 
Х Y, т.е. множество упорядоченных пар < х,у >, х X, у Y называется функцией тогда и только тогда, когда первые элементы этих пар не повторяются.
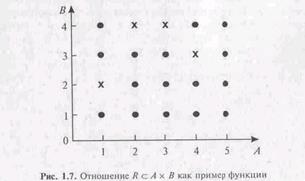
Пример. Отношение не является функцией, так как оно представлено следующими парами: <1,2>, <1,3>, <2,3>, <2,4>, <3,3>, <3,4>, <4,2>, <4,3>. Примером функции на том же декартовом произведении является отношение <1,2>,<2,4>, <3,4>, <4,3>.
Необходимо сказать, что требование неповторяемости первых элементов упорядоченных пар, представляющих отношение, гарантирует однозначность отображения, т.е. функцию f: Х 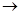Y.
При использовании термина «отображение» различают отображение Х в Y и отображение Х на Y.
В том случае, когда Х отображается на некоторое собственное подмножество Yс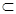 
Y, — это отображение Х в Y.
В противном случае, т.е. когда Yс=Y, — это отображение Х на Y. Оно называется сюръекцией.
Если для любых двух различных х1, и х2 функции f(x1) и f(x2) также различны, такая функция f называется инъективной.
Функция называется биективной или взаимно однозначной, если она съюрсктивна и инъективна.
В зависимости от того, какой характер имеют множества задания функций Х и множества ее значений Y, выделяют функции числовые (Х и Y — числовые множества), функционалы (множество Х — любой природы, а множество Y — числовое), операторы (множества X, Y — любой природы).
Пример. 1. Числовых функций являются все элементарные функции, например, у = х2, у = logх, у = sinх и т.д., а также их суперпозиции.
2. Функционал. Пусть в некотором городе N между двумя пунктами А и В имеется множество дорог X, каждой из которой поставлено в соответствие время t Т передвижения по ней автомобиля. Тогда множество пар <х,t>, х X, t T — функционал от t, определенный на множестве X.
3. Примером оператора может быть телефонная книга, в которой каждой фамилии абонента поставлен в соответствие один и только один номер его телефона.
Date: 2015-07-24; view: 387; Нарушение авторских прав