Оценка величины погрешности линейного однофакторного уравнения

В силу случайного отбора элементов в выборку случайными являются также оценки коэффициентов a и b уравнения регрессии.

1 В качестве меры суммарной погрешности выбрана величина:

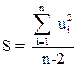. Для нашего примера S = 0.432

Поскольку 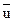(среднее значение остатков) равно нулю, то суммарная погрешность равна остаточной дисперсии:

2 Остаточная дисперсия находится по формуле:

Для нашего примера . Можно показать, что

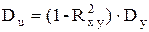
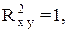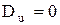
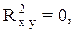Если то

то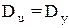

Таким образом,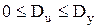

Легко заметить, что если

, то

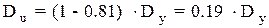
Это соотношение показывает, что в экономических приложениях допустимая суммарная погрешность может составить не более 20% от дисперсии результативного признака .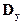

4 Стандартная ошибка уравнения находится по формуле:

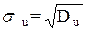, где

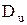- остаточная дисперсия. В нашем случае .

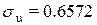5 Относительная погрешность уравнения регрессии вычисляется как:

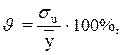
где стандартная ошибка;

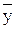- среднее значение результативного признака.

В нашем случае 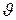= 7.07 %.

Если величина 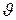мала и отсутствует автокорреляция остатков, то прогнозные качества оцененного регрессионного уравнения высоки.

6 Стандартная ошибка коэффициента b вычисляется по формуле:

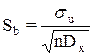
В нашем случае она равна .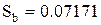

Для вычисления стандартной ошибки коэффициента a используется формула:

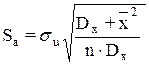
В нашем примере .

Стандартные ошибки коэффициентов используются для оценивания параметров уравнения регрессии.

Коэффициенты считаются значимыми, если

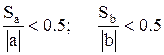
В нашем примере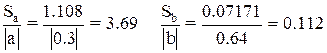

Коэффициент а не значим, т.к. указанное отношение больше 0.5, а относительная погрешность уравнения регрессии слишком высока - 26.7%.

Стандартные ошибки коэффициентов используются также для оценки статистической значимости коэффициентов при помощи t - критерия Стьюдента. Значения t - критерия Стьюдента содержатся в справочниках по математической статистике. В таблице 2.1 приводятся его некоторые значения.

Далее находятся максимальные и минимальные значения параметров (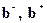) по формулам:

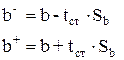
Т а б л и ц а 1

Date: 2015-07-24; view: 657; Нарушение авторских прав