Условия Гаусса – Маркова

1. Математическое ожидание случайного отклонения u_i равно нулю для всех наблюдений

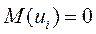
Данное условие означает, что случайное отклонение u_i в среднем не оказывает влияния на зависимую переменную. В каждом конкретном наблюдении случайное отклонение может быть либо положительным, либо отрицательным, но оно не должно иметь систематического смещения.

Фактически если уравнение регрессии включает постоянный член, то обычно бывает разумно предположить, что это условие выполняется автоматически, так как роль константы состоит в определении любой систематической тенденции в у, которую не учитывают объясняющие переменные, включенные в уравнение регрессии.

2. Дисперсия случайных отклонений постоянна для любых наблюдений.

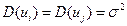
Данное условие подразумевает, что несмотря на то, что при каждом конкретном наблюдении случайное отклонение может быть либо большим, либо меньшим, не должно быть какой-то причины, вызывающей большую ошибку (отклонение).

Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений).

Величина 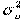, конечно, неизвестна. Одна из задач регрессионного анализа состоит в оценке стандартного отклонения случайного члена.

3. Случайные отклонения u_i и u_j являются независимыми друг от друга для i¹j.

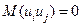
Выполнимость данной предпосылки означает отсутствие систематической связи между любыми случайными отклонениями. Т.е. величина и определенный знак любого случайного отклонения не должны быть причинами величины и знака любого другого отклонения.

Если данное условие выполняется, то говорят об отсутствии автокорреляции.

4. Объясняющие переменные не являются стохастическими.

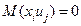
Случайное отклонение должно быть независимо от объясняющих переменных. Значение любой независимой переменной в каждом наблюдении должно считаться экзогенным, полностью определяемым внешними причинами, не учитываемыми в уравнении регрессии.

Предположение о нормальности

Наряду с условиями Гаусса—Маркова обычно также предполагается нормальность распределения случайного отклонения. Дело в том, что если случайное отклонение и нормально распределено, то так же будут распределены и коэффициенты регрессии. Предположение о нормальности основывается на центральной предельной теореме. В сущности, теорема утверждает, что если случайная величина является общим результатом взаимодействия большого числа других случайных величин, ни одна из которых не является доминирующей, то она будет иметь приблизительно нормальное распределение, даже если отдельные составляющие не имеют нормального распределения.

Теорема Гаусса-Маркова. Если предпосылки 1 – 4 выполнены, то оценки, полученные по МНК, обладают следующими свойствами:

1 Оценки являются несмещенными, т.е. отсутствует систематическая ошибка в определении положения линии регрессии. M(b₀)=b₀, M(b₁)=b₁. Это вытекает из того, что M(e_i)=0.

2 Оценки состоятельны, так как дисперсия оценок параметров при возрастании числа n наблюдений стремится к нулю: 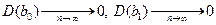. Другими словами, при увеличении объема выборки надежность оценок увеличивается (b₀ наверняка близко к b₀, b₁ - близко к b₁).

3 Оценки эффективны, т.е. они имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров, линейными относительно величин y_i.