Понятие оптимизационных задач и оптимизационных моделей

Экономико-математические задачи, цель которых состоит в нахождении наилучшего (оптимального) с точки зрения некоторого критерия или критериев варианта использования имеющихся ресурсов (труда, капитала и пр.), называются оптимизационными.

Оптимизационные задачи (ОЗ) решаются с помощью оптимизационных моделей (ОМ) методами математического программирования.

Структура оптимизационной модели состоит из целевой функции, области допустимых решений и системы ограничений, определяющими эту область.

Область допустимых решений - это область, в пределах которой осуществляется выбор решений. В экономических задачах она ограничена наличными ресурсами, условиями, которые записываются в виде системы ограничений, состоящей из уравнений и неравенств.

Если система ограничений несовместима, то область допустимых решений является пустой. Ограничения подразделяются на:

а) линейные (I и II) и нелинейные (III и IV) (рис.1);

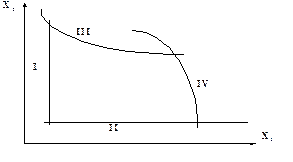
Рис. 1. Линейные и нелинейные ограничения

б) детерминированные (А,В) и стохастические (группы кривых 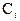) (рис. 2).

Рис. 2. Детерминированные и стохастические ограничения

Стохастические ограничения являются возможными, вероятностными, случайными.

Оптимизационные задачи решаются методами математического программирования, которые подразделяются на:

· линейное программирование;

· нелинейное программирование;

· динамическое программирование;

· целочисленное программирование;

· выпуклое программирование;

· исследование операций;

· геометрическое программирование и др.

Главная задача математического программирования - это нахождение экстремума функций при ограничениях в форме уравнений и неравенств.

Рассмотрим оптимизационные задачи, решаемые методами линейного программирования.

Date: 2015-07-24; view: 567; Нарушение авторских прав