
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Есеп шығару үлгісі. №1.Дж.Томсон моделіндегі бір электронды атомныңтербеліс жиілігін табу керек
|
|
№1. Дж.Томсон моделіндегі бір электронды атомныңтербеліс жиілігін табу керек.
Берілгені:
N=1
Тербеліс жилігін табу керек.
Шешуі: Томсонның моделі бойынша атом оң жəне терісэлектронмен зарядталған сфера. Оның зарядтары көлем ішінде бірқалыпты орналасады. Сондықтан атом бейтарап.
Атом центрінен r қашықтықтағы электронға f – күші əсер етеді.
| f= (-e)E= - | r | kr | (1) | |||||||
| k= | R | (2) | ||||||||
| Ал есептің шарты бойыншаR электрон тепе-теңдік қалпынан | ||||||||||
| ауытқып тербелсе, оның тербеліс жиілігі | ||||||||||
| (3) | ||||||||||
~ 43 ~
болатыны механика бөлімінен белгілі жəне
| (4) | |||||||||
| (2) | (3) - ге қойсақ, онда | ||||||||
| (5) | |||||||||
| мұндағы e – электрон заряды.Rm - электрон массасы. R – атом | |||||||||
| радиусы. | |||||||||
| (4) | жəне (5) теңдіктерді теңестірсек, онда | ||||||||
| e 2 | (6) | ||||||||
| mR 3 | |||||||||
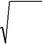 №2. Томсон моделіндегі бір электронды атом,қанша
№2. Томсон моделіндегі бір электронды атом,қанша
спектрлік сызыққа сəулеленеді? Толқын ұзындығы = 5000 А0 сəуле шығару үшін, атом радиусы қандай болу керек?
| Берілгені: | |||||||||||||||||||
| = 5000 | = 0,5 | ||||||||||||||||||
| Табу керек:R -? | |||||||||||||||||||
| Шешуі:AЭлектронға10матом центрінен центрге тартқыш жəне | |||||||||||||||||||
| квазисерпімді күш əсер етуге тиіс: | |||||||||||||||||||
| f= -kr = - | (1) | ||||||||||||||||||
| R | |||||||||||||||||||
| r=x; ауытқу шамасы. | |||||||||||||||||||
| k= m | онда f=- m r; бұл күш электр тарапынан əсер | ||||||||||||||||||
| ететін күшке; тең, онда | m | r | (2) | ||||||||||||||||
| e)E = - | |||||||||||||||||||
| f=(- | R | ||||||||||||||||||
| (3) | |||||||||||||||||||
| Гармониялық тербелістегі электронR | бір жиілікте | тербеледі, | |||||||||||||||||
| онда: | (4) | ||||||||||||||||||
| = | (5) | ||||||||||||||||||
| R | |||||||||||||||||||
| немесе = | (6) | ||||||||||||||||||
| )1/3 =; | 1,25 | ||||||||||||||||||
| онда R= ( | |||||||||||||||||||
| мұндағы, e | – заряд; | тыныштық массасы; с – жарық | |||||||||||||||||
| ; | м; |
 жылдамдығы; – толқын ұзындығы; R – атом радиусы.
жылдамдығы; – толқын ұзындығы; R – атом радиусы.
~ 44 ~
№3. ЗарядыZeядроны альфа бөлшегімен атқылағандабөлшектің ауытқу бұрышы (θ) ең жақын келу (нысаналы)
қашықтығына () байланысты екендігін мына формулада көрсетілген:
| сtg Ө | . Осы формуланы дəлелдеңдер. | |||
| МұндағыZ | альфа бөлшегінің массасы, | - оның |
жылдамдығы.
Шешуі: Резерфордтың байымдауы бойынша атом зарядтаржүйесінен тұрады, оның центрінде, ауыр заряды (+Ze), өлшемі
| (радиусы) | см ядро орналасқан. Бөлшек ядроға жақын | |||||
| оған кулондық күш əсер етеді: | ||||||
| келгенде, | = | Z | (1) | |||
 Бөлшектің траекториясы гипербола болады. Ауытқу бұрышы
Бөлшектің траекториясы гипербола болады. Ауытқу бұрышы
– Ө, ең жақын келу нысаналы қашықтығы -. Бөлшектің нысаналы қашықтығы ядро жазықтығына жақын келген сайын, ауытқу бұрышы (Ө) артады.
Энергияның сақталу заңы бойынша ядродан қашықтаған бөлшектің импульс шамасы (Р), шашырағанға дейінгі импульсына (Р) тең (P = P).
Шашырау нəтижесінде импульс өсімшесі Р = 2P Sin Ө = 2m Sin Ө (2)
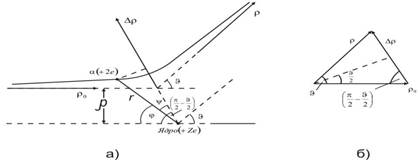
| Ал Ньютонның II заңы бойынша Р = dt | (3) |
мұндағы - Р бағытындағы күш векторының проекциясы. Онда = - Ө -
~ 45 ~
| n = сos = Sin (+ Ө) = | Z | Sin (+ Ө) | (4) | |||||||||||||||||||||||
| Осы (4)-ті (3)-ші теңдікке қойсақ, онда | ||||||||||||||||||||||||||
| = | Ө | S | Ө | (5) | ||||||||||||||||||||||
| Альфа бөлшегіне əРсер | ететін күш центрлік, олай болса альфа | |||||||||||||||||||||||||
| 2 e | ||||||||||||||||||||||||||
| бөлшегінің | импульс моменті тұрақты | ( | ), | бастапқы | ||||||||||||||||||||||
| күйінде қалады. | алмастырсақ, онда | |||||||||||||||||||||||||
| шешіледі. | ; | = | M | const | ||||||||||||||||||||||
| r | · | |||||||||||||||||||||||||
| интеграл оңай | M ө | m | Ө | Ө | ||||||||||||||||||||||
| = | Sin | (6) | ||||||||||||||||||||||||
| P | Z | d | Z | 2сos | ||||||||||||||||||||||
| (2) мен (6) теңдеуді теңестірсек | Z | 2сos | Ө | 2m | Sin | Ө ; | ||||||||||||||||||||
| ctg | m 2 | (7) | ||||||||||||||||||||||||
| 2 ze 2 | ||||||||||||||||||||||||||
| Жауабы:сtg | Ө | |||||||||||||||||||||||||
| = | . | |||||||||||||||||||||||||


 №4. а)Резерфорд тəжірибесіндегі альфа бөлшектіңкинетикалық энергиясы EK 8,0 Мэв болса. Алтын атомының (Z = 79) ядросына, альфа бөлшегі қаншалықты жақын келе алады (қандай r қашықтыққа дейін жақын келеді)?
№4. а)Резерфорд тəжірибесіндегі альфа бөлшектіңкинетикалық энергиясы EK 8,0 Мэв болса. Алтын атомының (Z = 79) ядросына, альфа бөлшегі қаншалықты жақын келе алады (қандай r қашықтыққа дейін жақын келеді)?
б) Резерфорд тəжірибесінде алтын фольга алынған деп есептесек, альфа бөлшектер Ө 90 бұрыштарға шашырау үшін () ең жақын келу (нысаналы) қашықтық қандай болатынын есептеп табу керек.
в) Осы шарттағы ядроның тиімді қимасы (əсерлесу қимасы) қандай шамада болады?
г) Алтын фольганың қалыңдығы d = 6 10 м болғандығы Ө 90 немесе одан үлкен бұрыштарға ауытқитын альфа бөлшектердің салыстырмалы санын анықта.
Берілгені:
E 8,0 Мэв
Z = 79
Табу керек: а) r -?б) -?в) -?г) n -?
~ 46 ~
Шешуі: а)Ядроға ең жақын аралыққа келгенде альфабөлшектің кинетикалық энергиясы (E), ядро жүйесінің потенциалдық энергиясына ауысады:
| = | Z | ; | (1) | |||||
| r = | (2) | |||||||
| E | ; | |||||||
| Z | ||||||||
 Осы теңдеуден r-ді табамыз.
Осы теңдеуден r-ді табамыз.
| , | , | , | , | = | 2,8 | . | r=2,8 | |||||||||||
| 10 м | м | · | ||||||||||||||||
| Сонда | алтын | атом | ядросының | радиусы | шамасында | |||||||||||||
| немесе бұдан кішімəнге тең болады, | радиусынан | есе | ||||||||||||||||
| кіші. | ол атом | |||||||||||||||||
| б) r – мəні үшін Ө 90 болса, онда ең жақын келу | ||||||||||||||||||
| қашықтығы: | ctg Ө | 1,48 10 | м. =1,48·10 | м | ||||||||||||||
| = | ctg Ө = | EK | ||||||||||||||||

 в) Ө 90 болғандағы ядроның тиімді қимасын () табамыз.
в) Ө 90 болғандағы ядроның тиімді қимасын () табамыз.
6,87·10 м
г) Бірлік көлемдегі ядросанын мына формуламен табуға болады:
| n = d | ; n=5,9 | алтынның тығыздығы; | |||||||||||||||
| d = 1,93 | кг/ | ||||||||||||||||
| - м | |||||||||||||||||
| M = 0,19710кг / | моль – мольдық масса; | ||||||||||||||||
| м | |||||||||||||||||
| = 6,02 | -Авогадра тұрақтысы | в) = | |||||||||||||||
| Жауабы:а) r | = 2,8 | ; | б) = | ||||||||||||||
| NA | 5,9 | м | . | 1,48 10 | м; | ||||||||||||
| 6,87 10 м | ; г) n = | м | |||||||||||||||
№5. Резерфорд–Бор моделін пайдаланып,электронныңорбита бойындағы қозғалыс жылдамдығын қорытып шығарып, сутегі атомының бірінші жəне екінші дөңгелек орбитадағы жылдамдығын анықта.
~ 47 ~
Берілгені:
n 1
n 2
Табу керек: 1-?2-?
Шешуі: Дөңгелек орбита бойымен қозғалған электронғацентрден тепкіш күш жəне Кулондық күш əсер етеді. Ол күштер электронның стационар орбита бойымен қозғалуын қамтамасыз етеді, онда олар өзара тең.
| Fц | ; | (1) | |||
| ; (2) | |||||
| Z | |||||
| Fкл |
екеуін теңестіріп, одан жылдамдықты анықтаймыз.
Z; =; (3)



Бор постулаты бойынша электронның импульс моменті:
| m r | n | (4) | |||||||||||||||||||||||
| (5) | |||||||||||||||||||||||||
| r(5) теңдікті (3) теңдікке апарып қойсақ: | |||||||||||||||||||||||||
| = | Z | = | Z | яғни | Z | ||||||||||||||||||||
| Жауабы: Егерn = 1 | болса, | ;онда | Z | 2,19; | Мм/с. | ||||||||||||||||||||
| ал n = 2 болса, онда | Z 1,09 М м/с. | ||||||||||||||||||||||||
№6. Электронның стационар орбитасы орнықты күйдеболады. Квантталу шарты бойынша электрон орбитаcының радиусының мүмкін формуласын қорытып шығарып, сутегі атомы үшін электронның бірінші жəне екінші орбиталарының радиусын тап.
| Берілгені: | n,n | ||||||
| Табу керек: | |||||||
| Шешуі:Алдыңғыr?r | есептердегідей? | , | электронның импульс | ||||
| моменті: | m r | n | |||||
| ; | (1) | ||||||
~ 48 ~
| m r | = n | ; | ||||
| Z | ; |

(3) теңдіктегі жылдамдықтың мəнін (1) теңдікке қойсақ:
m Z r =;


одан
(2)
(3)
(4)
| r = | Z | ||||||||
| Жауабы:Егер | = 1 | ||||||||
| болса, | онда | ||||||||
| n 2 болса, онда r | |||||||||
| 212,4 Пм. | |||||||||

(5)
53,1 Пм; ал
№7. Əрбір электрондық орбита белгілі энергетикалықдеңгеймен анықталады да, электронның толық энергиясы кинетикалық жəне потенциалдық энегиялар жиынтығынан тұрады.
Осы n – орбитадағы толық энергияны қорытып шығарыңдар.
Шешуі:
| E = E | EP | (1) | ||
| E | (2) | |||
Алғашқы есептерге байланысты дөңгелек орбита бойымен қозғалған электронға, кулондық жəне центрден тепкіш күштер əсер етеді. Бор постулаты бойынша электронның импульс моментін тұрақты мəндермен анықтауға болады. Сонда k – орбитадағы электронның жылдамдығы:
| = | Z | (3) | |||||||
| (3) теңдікті (2)теңдікке қойсақ,; онда | |||||||||
| K | Z | ; | (4) | ||||||
| ; | (5) | ||||||||
| радиусы | |||||||||
| n – орбитаның | E | r | Z | ||||||
 ~ 49 ~
~ 49 ~
Ал потенциалдық энергия:
g a; h;
EP mgh a = m; (6)
(3) теңдікті (6) теңдікке қойсақ:
| Сонда толық | энергия: | Z | ; | ||||||||
| EP | |||||||||||
| E= | Z | - | Z | Z | ; E = - | Z | |||||
| E=- , | эв |





(7)
; n = 1, 2, 3…
n-нің мəндерін қою арқылы əрбір орбитадағы электронның толық энергияларын анықтаймыз.
№8. Негізгі күйдегі сутегі атомының энергиясы12,09эв тең,фотон арқылы қоздырғанда, электрон орбитасының радиусы қанша есе артады?
Берілгені: m = 1
Eф = 12,09 эв
| Табу керек:n -? | ; (1) | ||||||||||||||||||||||||||
| Шешуі:Фотонның энергиясы? | |||||||||||||||||||||||||||
| C | |||||||||||||||||||||||||||
| Толқындық санның – толқын | ұзындықпен байланысы: | ||||||||||||||||||||||||||
| Еф | h | h | |||||||||||||||||||||||||
| = | ; | RZ | ; (2) | ||||||||||||||||||||||||
| - Бальмердің əмбебап формуласы. Сутегі үшін Z=1; | |||||||||||||||||||||||||||
| Сонда E = | с | = R h с | . | ||||||||||||||||||||||||
| Мұндағы, m = 1, 2... ал n = m + 1; | |||||||||||||||||||||||||||
| m = 1 болса, E = Rhс - | R с | R с | . | ||||||||||||||||||||||||
| n = | R с | 2,956 | ; | Rhс | E | ||||||||||||||||||||||
| R с E | |||||||||||||||||||||||||||
| ~ 50 ~ |





Есептің шарты бойынша қозған күйдегі радиусы, негізгі күйдегі орбита радиусынан қанша есе артық болады?
| r | ;r | ; | Z | 9 есе. | ||||||||||
| Z | Z | Z | ||||||||||||
| №9.Сутегі атомының ядросын, | радиусы | см |


 rБ 0,53 10
rБ 0,53 10
шеңбер бойымен айналғанда электрон, сəуле шығару арқылы энергиясы кеміп отырса, онда ол қанша уақыттан соң ядроға құлап түседі?
Шешуі:
Электрон кез келген уақыт мезетінде шеңбер бойымен бірқалыпты қозғалады деп алайық. Сонда Ньютонның II заңы бойынша: F = ma
| ; | (1) | ||||||||||||
| (2) | |||||||||||||
| (2) теңдіктің екі жағын | да екіге бөліп жіберсек, сонда | ||||||||||||
| m | ; | ||||||||||||
| E | (3) | ||||||||||||
| бұл кинетикалық энергияны береді. | |||||||||||||
| Ал ядро өрісіндегі электронның толық энергиясы | |||||||||||||
| E = | ; | (4) | |||||||||||
| электродинамика | |||||||||||||
| Классикалық | E | EP |
зарядталған бөлшектің сəулеленуге кеткен бірлік уақыт шығыны:
10 сек
| = - | ; – үдеуі. | (5) | ||||||||||||||||||
| (3) теңдікпен (4) теңдікті ескере отырып, (5) теңдікті | ||||||||||||||||||||
| ; | (6) | |||||||||||||||||||
| r мен e айнымалыларды ажыратып, | ||||||||||||||||||||
| dt; | (7) | |||||||||||||||||||
| (7) теңдікті интегралдаймыз. | ||||||||||||||||||||
| r; r | dr | |||||||||||||||||||
| Сонда | ден 0 –ге дейін, ал t; 0 – ден - ге дейін: | |||||||||||||||||||
| = | 1,5 10 | с болады. | ||||||||||||||||||
| №10.Электрон гармониялық тербеліске жақын,жиілікпен | ||||||||||||||||||||
| ( | тербеліп, өшетін тербеліске айналады. | Қанша |
уақыттан кейін (∆t) ол өзінің бастапқы энергиясының 0,9 бөлігін жоғалтады.
~ 51 ~
Берілгені:
10 сек
0,9

Табу керек: t-?
Шешуі: Классикалық электродинамика заңдарына сүйенсек,тербелген электронның онда шығын болған энергиясы мынадай формуламен өрнектеледі:
| E | (1) | ||||||
| мұндағы, Е - энергиясы, - электрон жылдамдығы, | - үдеуі. |
 Егер электронның тепе-теңдік ауытқуы:
Егер электронның тепе-теңдік ауытқуы:
(2)
(3)
(4)
мұндағы, х - ауытқу шамасы, ω - дөңгелектік жиілік, а - тербеліс амплитудасы, онда электронның толық энергиясы
| (5) | |||||||||||||||||||||||||||
| Бірлік уақыттағы орташа энергия шығыны: | |||||||||||||||||||||||||||
| (5) | теңдіктен | ω a; | (6) | ||||||||||||||||||||||||
| E | (7) | ||||||||||||||||||||||||||
| (7) | теңдікті-(6) теңдікке | апарып қойсақ | |||||||||||||||||||||||||
| а | |||||||||||||||||||||||||||
| · | · | ·2 | · | (8) | |||||||||||||||||||||||
 Олай болса, электронның энергиясының орташа өзгеруі мынадай түрде өрнектеледі:
Олай болса, электронның энергиясының орташа өзгеруі мынадай түрде өрнектеледі:
(9)


Бастапқы энергия мəнін Е0 деп белгілесек, онда уақыт:
| t | 3mc | ln | E | ; | |
| 2e ω | E |

 ~ 52 ~
~ 52 ~


сан мəндерін қойсақ, онда
2 ·4 1,9·10 сек;



m - электрон массасы, c - жарық жылдамдығы, e - электрон заряды, - жилігі, E0 - бастапқы энергиясы.
№11. Сутегімен дейтерий туралы мəлімет бойынша Ридбергтұрақтысы:
| RH | 109677,576 | 0,012 см | ; | |||||
| массасы: | 0,012 см | ; | ||||||
| ал атомдық RD | 109707,419 | |||||||
| H | физикалық шкала бойынша. | |||||||
| 1,009142 | 0,000003 | |||||||
| Фарадей тұрақтысы: | ||||||||
| D | 2,014735 | 0,000006 | ·10 бірл.CGSE· моль | |||||
| F | Ne | 2,89366 | 0,00003 | |||||
| 9652,19 0,11 бірл.CGSM моль | ||||||||
(физикалық шкала бойынша) Осы шартты пайдалана отырып, электрон үшін табу керек.

Шешуі: Сутегімен дейтерий үшін Ридберг тұрақтысы:
;; (1)




мұндағы, МН жəне МD – сутегі мен дейтерийдің ядро массалары, осы (1) теңдіктен:
| (2) | |||||||||||||||||||
| осы теңдіктің | екі жағында (е) | зарядқа | <