
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Сутегі атомының эллипстік орбитасы
|
|
Эллипстік орбитамен қозғалған электрон энергиясы үлкен жарты остің жəне кванттық санның мөлшерімен анықталмай, басқа жаңа кванттық сан (l) арқылы анықталсын. Онда орбитада орналасқан электрон энергиясына қандай жаңа əсерлесулер болатынын қарастырсақ, онда осы орбитада қозғалған электрон өте үлкен жылдамдықпен қозғалады, оның массасы жылдамдыққа байланысты өзгереді. Ал дөңгелектік орбитадағы электрон жылдамдығы тұрақты, олай болса орбитаның əр
~ 36 ~
бөлігінде электронның массасы өзгермей тұрақты болып қалады. Егерде электрон эллипстік орбитада қозғалса, орбитаның əр бөлігінде, жылдамдығы əртүрлі, яғни атом ядросына жақын келгенде жылдамдығы үлкен, ал ядродан алыстаса жылдамдығы баяулайды. Олай болса, эллипстік орбитада қозғалған электронның массасы да өзгереді. Сонда электрон жылжымайтын эллипстік осте ғана қозғалып қоймайды, өз жазықтығында айналатын эллипсте (1.11-сурет) айналады.
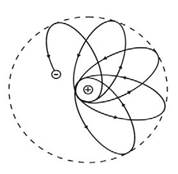
1.11-сурет
Бұл айналмалы қозғалыс үлкен болу үшін, эллипстік орбитаның үлкен жарты осі созылыңқы болуы керек жəне
а қатынасы неғұрлым кіші болған сайын, электрон массасының
 өзгеруі арта түседі.
өзгеруі арта түседі.
Олай болса, орбитадағы электрон энергиясын анықтағанда орбита мөлшерін ғана есепке алып қоймай оның формасында еске алып, орбита формасын анықтайтын шаманы да табу керек. 1.12-сурет бойынша электронның импульс моментін табамыз.
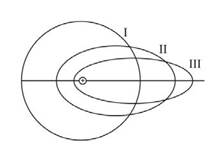
1.12-сурет
~ 37 ~
Бірінші күйдегі дөңгелек орбитадағы импульс моменті
| M | m a | (1.9.1) | |||

Екінші күйдегі, яғни эллипстік орбитадағы импульс моменті.
| M | m b | (1.9.2) | |||

Бірінші орбитадағы электронның толық энергиясы:
| E | m 2 | Ze 2 | Ze 2 | ||||||
| 1 | r | 2 r | (1.9.3) | ||||||
| 4 0 | 4 0 | ||||||||
Екінші орбитадағы электронның толық энергиясы:
| E | m 2 2 | Ze 2 | Ze 2 | (1.9.4) | |||||
| 4 0 | a | 4 0 | 2 a | ||||||
егер a r; 1 2 болса, онда (1.9.1) жəне (1.9.2) формуладағы импульс моментін тұрақты мəндер бойынша өрнектейік:
| M | m a n | h | (1.9.5) | |||

бұдан
| m | nh | (1.9.6) | ||
| 2 a | ||||
ал
| M | m b | (1.9.7) | |||

(1.9.6) формуланы (1.9.7) – формулаға қойсақ, онда
~ 38 ~
| M 2 | b n | h | (1.9.8) | |||||
| a | ||||||||
| Бұдан эллипстық орбитада қозғалған электронның элементар | ||||||||
| импульс моменті | h | -ге еселеніп квантталған болады. | ||||||
| (1.9.8) теңдіктегі n b l шамаға тең - | бұл орбиталдық | |||||||
| a |
кванттық сан, ол эллипстық траекториямен қозғалған электронның импульс моментін сипаттайды. Яғни l 0;1;2;
(n 1) мəндерге ие болып, эллипстық орбита формасын
сипаттайды. Мұндағы l 0 болса, электрон қозғалысы, атом ядросынан өтетін түзуге сəйкес келеді.
Классикалық механика бойынша мұндай қозғалыс болуы мүмкін емес. Ал кванттық механикада бөлшектер қозғалысы толқындық процесс, олай болса мұндай процеске рұқсат етіледі.
Сонымен эллипстық орбита екі кванттық санмен сипатталады, оның біреуі n – бас кванттық сан, екіншісі орбитаның үлкен жарты осі - а. Олар қозғалмайтын эллипстік орбитадағы электрон энергиясын сипаттайды, ал l -кванттық саны эллипстік жарты осьтерінің қатынастарын жəне өз жазықтығында қозғалған эллипстік орбита бойындағы электрон энергиясын анықтайды.
Мұндай жағдайлар электронды ядроға тартатын Кулондық күштен басқа күштер əсер етпесе энергиясы өзгермейді. Егер қандай да бір қосымша күш пайда болса, онда орбитаның үлкен жарты осі (а) өзгермейді, ал кіші жарты осі (в) өзгеріп, электрон əртүрлі энергияға ие болады. Бұл жағдайда толық энергия бас кванттық санмен (n), үлкен жарты осьтің өлшемдерінен басқа да параметрлерге, яғни - қосымша кванттық санға да (l) байланысты болады.
Date: 2015-07-24; view: 1029; Нарушение авторских прав