Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Луй – де – Бройль теңдеуі

⇐ ПредыдущаяСтр 15 из 106Следующая ⇒

 

Оптика бөлімінде жарықтың толқындық əрі корпускулалық қасиеттері болатынын анықтаған болатынбыз. Яғни интерференция жəне дифракция құбылыстары жарықтың толқындық табиғатын білдірсе, фотоэффект Комптон–эффектісі жарықтың корпускулалық, немесе кванттық қасиеттерін түсіндіреді. Толқындық теория тұрғысында жарық жиілік пен толқын ұзындығы арқылы, ал корпускулалық теория бойынша жарық фотонының белгілі энергиясы, массасы жəне импульсі арқылы сипатталады. Олар өзара байланысты болады. Корпускулалық теория бойынша жарық фотонының энергиясы (квант)

 

E hv h c (2.1.1)  
   
ф ф      
      ф    

Салыстырмалық теория бойынша энергия мен масса байланысты. Оны жарық фотонына қолдансақ, фотон энергиясы үшін:

 

E m c 2 (2.1.2)
ф ф  

 

Осы формуладан масса мен импульсті анықтасақ, ол

 

m Eф   hvф   h (2.1.3)  
с 2 c 2 c  
          ф    

 

Pф mфc hc   h (2.1.4)  
c    
  ф   ф    

~ 61 ~


Сонымен жарық фотонының массасы мен толқын ұзындығы арасын жарық жылдамдығы, ал импульспен толқын ұзындық арасын М. Планк тұрақтысы байланыстырып тұрады.

 

Олай болса жарықтың екі жақтылық қасиеттері болады, ондай қасиеттері электронға да тəн деген гипотезаны француз физигі Луй – де – Бройль ұсынды. Луй – де – Бройльдың пікірінше əрбір электронның қозғалысы бір толқындық процеске байланысты. Егер электрон жылдамдығы жарық жылдамдығынан аз болса (υ≤с), онда электрон импульсі мен толқын ұзындығының арасындағы байланысты (2.1.4)-формулаға ұқсас мынадай формуламен өрнектеуге болады:

 

P m h бұдан h (2.1.5)  
  m  
e e e    
    e   e    

Бұл формула де – Бройль формуласы деп аталады.

 

Егер электрон үдетуші электр өрісінде қозғалса, оның кинетикалық энергиясын мынадай түрде жазамыз:

m 2 eU бұдан 2 eU (2.1.6)  
e me  
   
       

 

мұндағы, U үдетуші потенциал, е – электрон заряды. (2.1.6) формуланы (2.1.5) формулаға қойсақ, онда

 

    h (2.1.7)  
   
e   2 meeU  
       

 

 

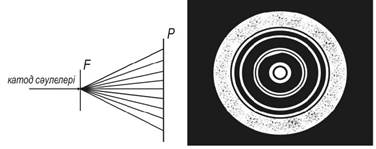
2.1-сурет

 

~ 62 ~


Егер электронның жылдамдығы үлкен болса (үдетуші потенциал 102 В), онда оның толқын ұзындығы (е=1,2·10-10м) кристалдардың атомдық жазықтықтарының арақашықтығына шамалас болады. Олай болса де Бройль толқындары үшін кристалдық тор - дифракциялық тор қызметін атқарады.

 

Осындай шапшаң электрондар жұқа металл фольгадан өткенде дифракция құбылысы байқалатынын алғаш ағылшын физигі Дж. Томсон анықтады. Оның жасаған тəжірибесінде разрядтық түтік ішінде қоздырылған катод сəулелерінің, жіңішке шоғы жолындағы металл фальгадан өткенде дифракцияланып,жолына перпендикуляр қойылған фотопластинка бетіне түседі. Сонда пластинка бетіне ортасы тұтасқан дағы бар, оның сыртында бірнеше концентрлік шеңберлер пайда болады (2.1-сурет) ол дифракциялық кескінге ұқсас болады. Бұл тəжірибе негізін Вульф – Брэггтер жасаған рентген сəулесінің дифракциясындағы


 

2 d sin n (2.1.8)

 

формуласы арқылы түсіндіруге де болады. Мұндағы n -нің əрбір мəніне бір конус сəйкес келеді. Дифракциялық көріністегі сақиналар мөлшері үдеткіш потенциалға тəуелді болады. Формуладағы (2.1.8) мен тұрақты, сонда бұрышының белгілі бір мəніне сəйкес бағыт бойынша шашыраған электрондар төбесіндегі бұрышы 2φ- ге тең конус бетімен таралады да (2.1.8) теңдіктегі n -нің əрбір мəніне бір конус сəйкес келеді. Бұл құбылыс электрондар шоғының толқындық қасиеті бар екендігін көрсетеді. Томсон тəжірибесін түсіндіру үшін Луй-де-Бройль мен Вульфа-Брэггтер формулаларын пайдаланып түсіндіреді.

 

Де-Бройль толқындары классикалық физикадағы толқындармен ұқсастыруға болмайтын, ерекше кванттық табиғаты бар толқындар. Луй-де-Бройль толқындарының мағынасын түсінуге жарықтың толқындық жəне корпускулалық қасиеттері елеулі көмек береді. Толқындардың табиғаты жөніндегі мəселені осы толқындар амплитудасының физикалық мағынасы ретінде қорытындылауға болады. Амплитуда орнына оның модулінің |А|2 квадратына пропорционал толқын

 

~ 63 ~


интенсивтілігін қарастыруға ыңғайлы болады. Өйткені оның энергиямен байланысқан квадраты, нақты шама болады.

 

Де-Бройль толқындарының берілген нүктедегі амплитуда-сының модулінің квадраты бөлшектің осы нүктеде табылу ықтималдығының өлшемі болып табылады.

 

Қарапайым бөлшектердің негізгі қасиеттерінің бірі олардың бөлінбейтін бүтін болуы жəне заряды бір денеден екінші денеге бөлінбейтіндігі. Бұл электрон заряды бөлінбейтіндігін көрсетеді.

 

Шапшаң электрондар шоғының өте жұқа металл пластикадан өткен кездегі дифракциясын ең алғаш 1927 жылы американ физигі Дэвиссон жəне Джермер байқады, ал 1928 жылы ағылшын физигі Томсон анықтады.

 


⇐ Предыдущая10111213141516171819Следующая ⇒





Date: 2015-07-24; view: 2649; Нарушение авторских прав


mydocx.ru - 2015-2024 year. (0.009 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию