
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Бор – Зоммерфельд кванттау ережелері. Бор теориясының қайшылықтары
|
|
Сутегі жəне сутегі тектес иондарды түсіндіруде Бор жетістіктері өте көп болғанымен, оның теориясында елеулі кемшіліктері болды. Мысалы, сутегінен кейінгі химиялық
~ 39 ~
элемент, гелийдің атомы екі электроннан тұрады, оны Бор теориясы арқылы қарапайым жолмен түсіндірудің қиындықтары кездеседі. Өйткені барлық электрондар дөңгелек орбитамен қозғалғанда оларға центрден тепкіш күштер əсер етеді, ол күш арақашықтықтың квадратына кері пропорционал. Шын мəнінде электронның қозғалысына ядроның өз осінен айналуы да əсер етеді. Электронның осындай дөңгелек орбитамен қозғалуына түзетулер енгізуге тура келеді жəне электрондар тек дөңгелектік емес эллипстік орбитамен де қозғалады.
Бор теориясын қиындықтан шығарған неміс физигі А. Зоммерфельд болды. Зоммерфельд бойынша сутегі атомының электроны ядроны айнала эллипс бойымен қозғалады (1.13-сурет), ядро оның фокустарының біреуінде жатады, оның заряды +Ze, ал эллипстің үлкен жарты осі:
| a n 2 | rb | (1.10.1) | |||||
| z | |||||||
| кіші жарты осі | b nn | rb | (1.10.2) | ||||
| z | |||||||
| мұндағы, n – бас кванттық, ал | - азимуттық кванттық сан. Бас | ||||||
| кванттық сан | , мұндағы nr – радиустық кванттық сан. | ||||||
Эллипстің үлкен жарты осі тек бас кванттық санға, ал кіші жарты осі азимуттық кванттық санмен бас кванттық санға тəуелді болады. Бордың анықтауы бойынша азимуттық кванттық сан еш уақытта нөлге тең болмайды, олай болса, nφ=1,2,3,4---n, nr=0,1,2,3-- n-1, сонда сутегі атомы негізгі күйде болғанда nr=0; nφ=1; n=1 (n=0+1=1). Бұл жағдайда (1.10.1) жəне (1.10.2) теңдік бойынша:
| a 12 | rb | r | (1.10.3) | |||
| b | ||||||
| rb | ||||||
| ал b 1 1 | r | (1.10.4) | ||||
| b | ||||||
олай болса а=b=rb, яғни электронның бірінші орбитасы дөңгелек болады. Егер n=3 болса nr=1; nφ=2, онда электронның орбиталарының саны үшеу болады, оның екеуі эллипс ал біреуі дөңгелек (1.12-суретке сəйкес). Осы эллипстік орбитаның үлкен жарты осьтері бірдей, кіші жарты осьтері əртүрлі болады. Орбита
~ 40 ~
саны бас кванттық санға тең болады, бірақ олардың формалары бірдей болмайды. Ал оларға сəйкес келетін энергия шамалары, Зоммерфельд теориясы бойынша бірдей болады.
| E | mz 2 e 4 | ||
| 8 02 n | 2 h 2 | ||
| (1.10.5) |
 Электрон дөңгелектік орбитамен қозғалғанда, оның кинетикалық жəне потенциалдық энергиясы өзгермейді. Егер электрон эллипстік орбитамен қозғалса, онда электронның ядродан қашықтығы өзгеріп отыратындықтан, потенциалдық энергия үздіксіз өзгереді. Олай болса потенциалдық энергияның өзгеруіне байланысты кинетикалық энергиясы да өзгереді, онда электрон жылдамдығының шамасы да өзгереді. Сонда электронның эллипстік орбитадағы толық энергиясы немесе ядро өрісіндегі потенциалдық энергиясы:
Электрон дөңгелектік орбитамен қозғалғанда, оның кинетикалық жəне потенциалдық энергиясы өзгермейді. Егер электрон эллипстік орбитамен қозғалса, онда электронның ядродан қашықтығы өзгеріп отыратындықтан, потенциалдық энергия үздіксіз өзгереді. Олай болса потенциалдық энергияның өзгеруіне байланысты кинетикалық энергиясы да өзгереді, онда электрон жылдамдығының шамасы да өзгереді. Сонда электронның эллипстік орбитадағы толық энергиясы немесе ядро өрісіндегі потенциалдық энергиясы:
| U | 1 Ze 2 | (1.10.6) | ||||||||
| r | ||||||||||
| ал толық энергиясы Ep | Ze 2 | |||||||||
| 4 0 2 a | (1.10.7) | |||||||||
| E | mZ | 2 e 4 | (1.10.8) | |||||||
| 8 02 | n 2 h 2 | |||||||||
(1.9.6) жəне (1.9.8) формулаларды салыстыра отырып, мынадай қорытындыға келеміз. Егер эллипстік орбитаның үлкен жарты осі дөңгелектік орбитаның радиусына тең болса, онда осы орбиталарда айнала қозғалған электронның энергиялары тең болады.
~ 41 ~
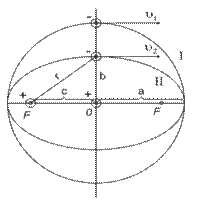
1.13-сурет
А. Зоммерфельдтің анықтауынша квантталған эллипстік орбитаның үлкен жарты осі мына шартты қанағаттандырады:
| an | 0 n 2 h 2 | (1.10.9) | |
| 2 mze 2 | |||
Егер электрон қозғалған эллипстік орбитаның үлкен жарты осі бірдей, ал кіші жарты остері əртүрлі болса, онда олардың энергиясы жəне оған сəйкес сипаттайтын кванттық саны (n) бірдей болады. Бұл процесс электронға сырттан ешқандай күш əсер етпесе осы күйде қала береді (кулондық тартылыс күштен басқа).
Егер қосымша күш пайда болса, онда үлкен жарты ос сол күйінде қалады да кіші жарты осі əртүрлі болып, электрон əртүрлі энергияға ие болады.
Классикалық электродинамика тұрғысынан қарастырсақ, онда тұйық орбита бойымен қозғалған электрон, тұйық сыммен жүрген электр тогына ұқсас, оның да магниттік моменті болады. Онда электронның магниттік моменті электронның орбиталдық импульс моментіне пропорционал, яғни:
| 0 e P | (1.10.10) | |||
| l | 2 m l |
~ 42 ~
| мұндағы, | 0 | - | вакуумдағы | магниттік | өтімділік | |||
| 0 | 1,257 10 6 Гн / м | |||||||
| Р l – | электронның | орбиталдық | импульс | моменті, ол | ||||
| P n | h | |||||||
| l | ||||||||
Р l -дің мəнін (1.10.10) формуласына қойсақ:
| l | 0 eh n | Б | n | (1.10.11) | ||||
| 4 m | ||||||||
мұндағы, Б 0 eh - Бор магнетоны деп аталады, оның сан
4 m
мəні
| Б | 1,257 10 6 1,6 10 19 6,625 10 34 | 1,15 10 29 Вc м | |
| 4 3,14 9,1 10 31 |
Бор магнетоны тұрақты, атом құрылысында ол маңызды рөл атқарады.
Date: 2015-07-24; view: 1436; Нарушение авторских прав