Математическая модель и ее анализ. Критерий оптимальности R представляет собой суммарные затраты на эксплуатацию теплообменника в единицу времени и может быть записан в виде:

Критерий оптимальности R представляет собой суммарные затраты на эксплуатацию теплообменника в единицу времени и может быть записан в виде:

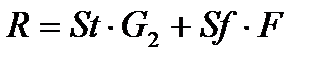или 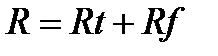(3.11)

где 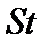- стоимость единицы массы хладоагента; 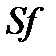- стоимость единицы поверхности теплообмена, 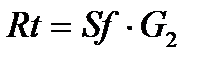- эксплуатационные затраты, 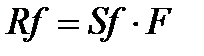- капитальные затраты.

Для того чтобы получить возможность использовать критерий оптимальности 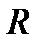для выбора оптимальной поверхности теплообмена 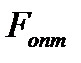и оптимальной величины расхода хладоагента 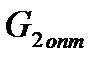, необходимо из уравнений математического описания теплообменника найти связь между переменным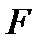и и .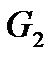

Запишем уравнение общего теплового баланса теплообменника:

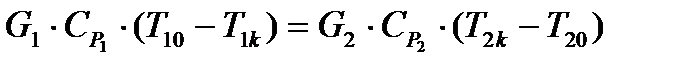(3.12)

Полученное уравнение запишем относительно переменной :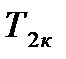

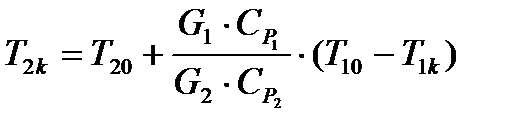(3.13)

Запишем выражения теплового баланса второго теплоносителя (хладоагента) с учетом источника тела:

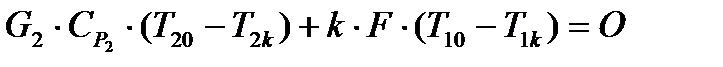(3.14)

Полученное уравнение запишем относительно переменной :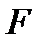

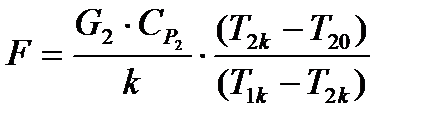(3.15)

Таким образом, мы получили систему уравнений, определяемые переменные которой являются функциями расхода хладоагента 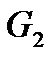. Решение задачи оптимизации сводится к определению такого значения расхода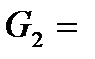 , при котором функция суммарных затрат имеет минимум.

1.

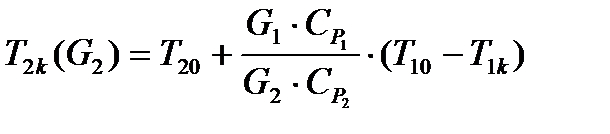
2. 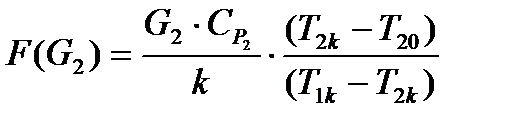(3.16)

3.

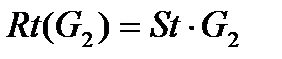
4.

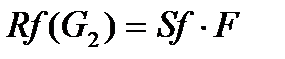
5.

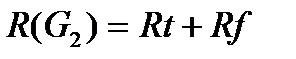
При нахождении минимума функции необходимо учитывать следующие ограничения.

Расход хладоагента 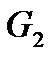и поверхность теплообменника 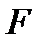могут принимать значения только больше нуля. Конечная температура хладоагента 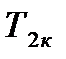не может быть больше конечной температуры первого теплоносителя .

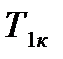Большое значение для сходимости итерационного процесса решения задачи оптимизации имеет правильный выбор начального значения переменной 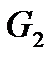. Из уравнения 1 следует предварительно определить, при каких значениях 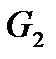конечная температура хладоагента 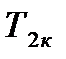становится больше конечной температуры первого теплоносителя 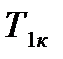, что физически невозможно. Поэтому начальное приближение для переменной 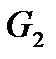должно быть принято больше этого значения.

Date: 2015-07-24; view: 441; Нарушение авторских прав