Работа №3. Технико-экономическое моделирование и оптимизация

Можно выделить в отдельную группу задачи моделирования и оптимизации, когда в качестве целевой функции используются не химико-технические, а экономические критерии.

Наиболее типичными являются следующие задачи.

1. Составление смесей (достижение заданного качества смеси при наименьших расходах).

2. Планирование выпуска продукции (максимизация выпуска продуктов при ограничениях на сырье и другие ресурсы для их производства).

3. Загрузка оборудования (минимизация издержек при выпуске продукции на установках разной мощности и стоимости).

4. Транспортная задача (минимизация затрат на поставку сырья от разных производителей).

С математической точки зрения эти задачи относятся к задачам, решаемым методами линейного и нелинейного программирования. В программе Excel эти методы реализованы в надстройке Поиск решения. Математические аспекты методов будут рассмотрены в примерах решения типовых задач.

Пример 3.1. Планирование оптимального выпуска продукции

Если под ресурсами понимать все, что используется в процессе производства: финансы, оборудование, сырье, материалы, людей (в смысле заработной платы), то значительное число задач с позиции экономических критериев можно рассматривать как задачи планирования ресурсов. Математической моделью таких задач является задача линейного программирования, которая является достаточно распространенной задачей принятия оптимальных решений. В данном примере задача будет сформулирована в самом общем виде. В разделе заданий для самостоятельной работы будут даны более конкретные формулировки постановки задачи.

Требуется определить, в каком количестве надо выпускать продукцию четырех типов Прод1, Прод2, Прод3, Прод4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье, финансы.

Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, прибыль, получаемая от реализации единицы каждого типа продукции, а там же наличие располагаемого ресурса приведено в табл. 3.1.

Таблица 3.1

Ресурс	Прод1	Прод2	Прод3	Прод4	Знак	Наличие
Прибыль					max	-
Трудовые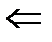
Сырье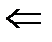
Финансы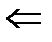

Составим математическую модель, для чего введем следующие обозначения:

X_j- количество выпускаемой продукции j-го типа, j=1-4;

b_i,- количество располагаемого ресурса i – го вида, i = 1-3;

а _{i j} –норма расхода i – го ресурса для выпуска единицы продукции j – го типа;

с _j – прибыль, получаемая от реализации единицы продукции j-го типа.

Как видно из табл. 3.1, для выпуска единицы Прод1 требуется 6х₁ единиц сырья, для выпуска Прод2 потребуется 5х₂ единиц сырья, для выпуска Прод3 потребуется 4х₃ единиц сырья, а для выпуска Прод4 потребуется 3х₄ единиц сырья. С учетом того, что запасы сырья ограничены 110 единицами, можно записать выражение для ограничения по сырью:

6х₁+5х₂+4х₃+3х₄ 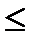110.

В этом ограничении левая часть равна величине потребного ресурса, а правая показывает количество имеющегося ресурса.

Аналогично можно составить ограничения для остальных ресурсов и написать зависимость для целевой функции. Тогда математическая модель задачи будет иметь вид:

F=60х₁+70 х₂+120 х₃+130 х₄ 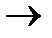max

х₁+ х₂+ х₃+ х₄ 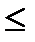16

6х₁+5х₂+4х₃+3х₄ 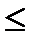110 (8.1)

4х₁+6х₂+10х₃+13х₄ 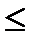100

x_j 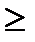0 j = 1-4

Date: 2015-07-24; view: 709; Нарушение авторских прав